O Material Dourado é um dos muitos materiais idealizados pela médica e educadora italiana Maria Montessori para o trabalho com Matemática. Sua idealização seguiu os mesmos princípios montessorianos para a criação de qualquer um dos seus materiais, a educação sensorial:

►desenvolver na criança a independência, confiança em si mesma, a concentração, a coordenação e a ordem;

►gerar e desenvolver experiências concretas estruturadas para conduzir, gradualmente, a abstrações cada vez maiores;

►fazer a criança, por ela mesma, perceber os possíveis erros que comete ao realizar uma determinada ação com o material;

►trabalhar com os sentidos da criança.

O Material Dourado Montessori foi criado com o intuito de destinar-se a atividades que auxiliassem o ensino e a aprendizagem do Sistema de Numeração Decimal-Posicional e dos métodos par a efetuar as operações fundamentais (ou seja, os algoritmos). Mas felizmente, essa utilização evoluiu e hoje esse material pode ser utilizado para o estudo de frações, conceituação e cálculo de áreas e volumes, trabalho com números decimais, raiz quadrada e outras atividades criativas.

No ensino tradicional, as crianças acabam “dominando” os algoritmos a partir de treinos cansativos, mas sem conseguirem compreender o que fazem. Com o Material Dourado a situação é outra: as relações numéricas abstratas passam a ter uma imagem concreta, facilitando a compreensão. Obtém-se, então, além da compreensão dos algoritmos, um notável desenvolvimento do raciocínio e um aprendizado bem mais agradável.

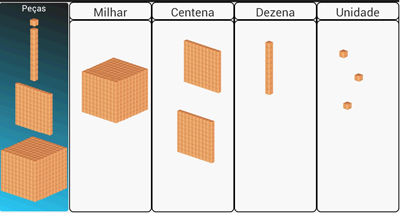
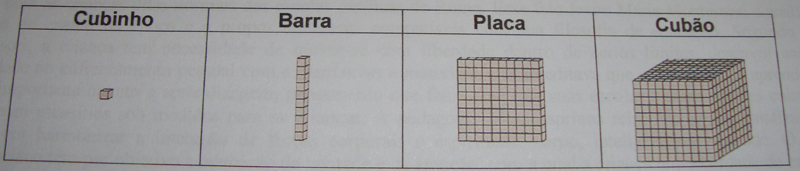
A forma utilizada hoje para o material dourado foi um pouco modificada em relação à forma original proposta por Montessori. Lubienska de Lenval, seguidora de Montessori, construiu seu material em madeira, diferente apenas no aspecto visual do material construído por contas douradas de Montessori. O Material Dourado Montessori é, então, constituído por cubinhos, barras, placas e cubão (Figura 1). Essa nomenclatura é muito mais propícia do que unidade, dezena, centena e unidade de milhar, devido a outras aplicações onde os elementos teriam classificação diferenciada.

 Figura 1: Material Dourado Montessori

 

A Figura 2 mostra que o cubão é formado por 10 placas, que a placa é formada por 10 barras e a barra é formada por 10 cubinhos. Esse material baseia-se em regras do nosso sistema de numeração. 

     Figura 2: Representação do cubão por 10 placas, da placa por 10 barras e da barra por 10 cubinhos

 

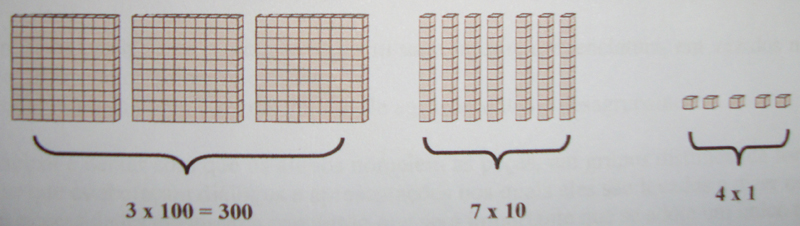
A Figura 3 mostra como se representa, com o material dourado, o número 374:

 

Utilizando o material, o professor notará em seus alunos um significativo avanço de aprendizagem. Em pouco tempo, estará enriquecendo e criando novas atividades adequadas aos seus alunos, explorando assim as inúmeras possibilidades desse notável recurso didático. É importante notar que os próprios alunos brincando com o material irão aprender conceitos primitivos da matemática.

 

Montessori

Maria Montessori nasceu na Itália, em 1870, e morreu em 1952. Formou-se em medicina, e nos anos iniciais deste século dedicou-se à educação de crianças excepcionais, que, graças à sua orientação, rivalizavam nos exames de fim de ano com as crianças ditas normais das escolas públicas de Roma. Esse fato levou Maria Montessori a analisar os métodos de ensino da época e a propor mudanças compatíveis com sua filosofia de educação. Segundo Maria Montessori, a criança tem necessidade de mover-se com liberdade dentro de certos limites, desenvolvendo sua criatividade no enfrentamento pessoal com experiências e materiais. Ela acreditava que o ambiente de aprendizagem era tão importante quanto a aprendizagem, pensamento que fazia com que suas escolas fossem lugares calmos, em ordem, com utensílios sob medidas para as crianças. A pedagogia Montessoriana relaciona-se à normatização que consiste em harmonizar a interação de forças corporais e espirituais, corpo, inteligência e vontade. O método Montessoriano tem por objetivo a educação da vontade e da atenção, com a qual a criança tem liberdade de escolher o material a ser utilizado, além de proporcionar a cooperação[1]. São alguns de seus princípios a aceitação do “ser” como “Pessoa Humana” – respeito ao educando, aceitação das diferenças individuais (físicas, ambientais, intelectuais e emocionais), deixando o educando livre para que, através de experiências e vivências diárias, ele possa se auto-educar e auto-disciplinar. Os materiais criados por Montessori têm papel preponderante no seu trabalho educativo, pois pressupõem a compreensão das coisas a partir delas mesmas, tendo como função estimular e desenvolver na criança um impulso interior que se manifesta no trabalho espontâneo do intelecto.

 

Trabalhando o conceito de número com o material Dourado

O trabalho com o material dourado se inicia com o reconhecimento do material. Neste momento o aluno pode manusear as peças da forma que quiser, fazer suas descobertas e estabelecer as suas relações. Em seguida procedem-se algumas atividades que, como proposto por Toledo (1997: p. 73), devem ser dispostas de forma progressiva a fim de se obter o máximo de resultados favoráveis estimulando a compreensão de conceitos de serão fundamentais para uma aprendizagem significativa, estando aí incluídos não somente as operações e representações com números, mas, principalmente o trabalho com conceitos de ordenação, inclusão hierárquica e conservação de quantidades, entre outros.

ATIVIDADES:

1) NOMENCLATURA E EQUIVALÊNCIA

Nesta atividade os nomes convencionais das peças são introduzidos (cubinho, barra, placa, cubão).

Objetivo: Fazer com que todos a partir deste momento utilizem uma mesma nomenclatura, em vez dos nomes particulares que cada um possa ter atribuído no primeiro contato; Estabelecer relações entre as peças e regras válidas de agrupamentos e desagrupamentos.

Metodologia: A estratégia principal é deixar com que os alunos nomeiem as peças, em grupos distintos, da forma que quiserem. Em seguida sugere-se que estabeleçam diálogos e apresentações nos quais eles são levados a dizer os nomes que adotaram e a partir de suas necessidades cheguem à conclusão que será importante que se adote um único padrão.

Em seguida passa-se à fase de estabelecer relações e, neste momento, podem ser feitos os seguintes questionamentos:

► Quantos cubinhos precisam enfileirar para forma uma barra?

► Quantas barras são necessárias para formar uma placa?

► Com quantas placas forma um cubão?

 2) JOGOS LIVRES

Objetivo: tomar contato com o material, de maneira livre, sem regras.

Durante algum tempo, os alunos brincam com o material, fazendo construções livres. O material dourado é construído de maneira a representar um sistema de agrupamento. Sendo assim, muitas vezes as crianças descobrem sozinhas relações entre as peças. Por exemplo, podemos encontrar alunos que concluem:

– Ah! A barra é formada por 10 cubinhos!

– E a placa é formada por 10 barras!

– Veja, o cubo é formado por 10 placas!

3) MONTAGEM

Objetivo: perceber as relações que há entre as peças.

O professor sugere as seguintes montagens:

– uma barra;

– uma placa feita de barras;

– uma placa feita de cubinhos;

– um bloco feito de barras;

– um bloco feito de placas;

O professor estimula os alunos a obterem conclusões com perguntas como estas:

– Quantos cubinhos vão formar uma barra?

– E quantos formarão uma placa?

– Quantas barras preciso para formar uma placa?

Nesta atividade também é possível explorar conceitos geométricos, propondo desafios como estes:

– Vamos ver quem consegue montar um cubo com 8 cubinhos? É possível?

– E com 27? É possível?

4) CONSTRUÇÕES

O professor pede para que cada um construa a figura que desejar e depois que contem quantos cubinhos foram utilizados na construção.

Objetivo: Neste momento os estudantes são levados a encontrar formas rápidas de contagem e para isto precisarão descobrir quantos cubinhos há em uma placa e no cubão, por exemplo.

Metodologia: O professor poderá sugerir as seguintes atividades:

►Contagem dos cubinhos da figura feita pelo aluno;

►Contagem dos cubinhos da figura do colega;

►Construção de figuras com um número limitado de cubinhos, podendo o aluno escolher que peça poderá utilizar.

5) DITADO

Objetivo: relacionar cada grupo de peças ao seu valor numérico.

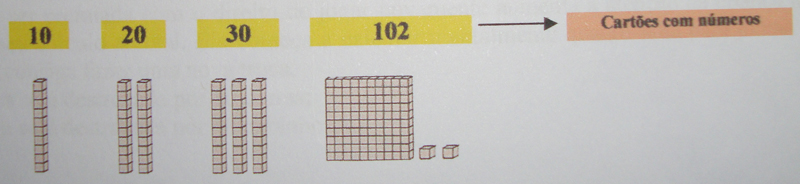
O professor mostra, um de cada vez, cartões com números. As crianças devem mostrar as peças correspondentes, utilizando a menor quantidade delas.

Variação: O professor mostra peças, uma de cada vez, e os alunos escrevem a quantidade correspondente.

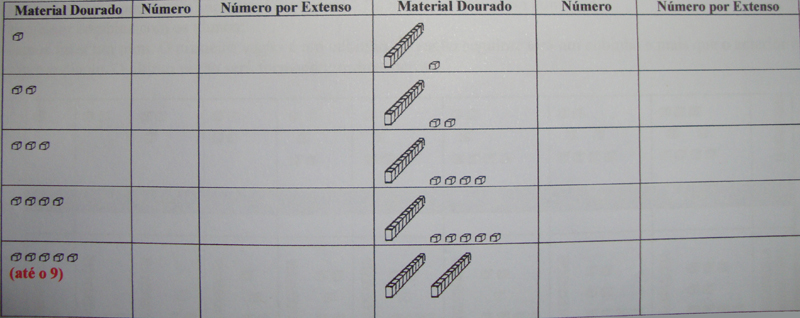
 6) REPRESENTAÇÕES

Vamos escrever em numerais e por extenso as representações com o Material Dourado:

Observação: Realizar outras atividades se necessário, com representações de centena e unidade de milhar (dependendo do nível de aprendizado da criança).

7) FAZENDO TROCAS

Objetivo: compreender as características do sistema decimal.

► fazer agrupamentos de 10 em 10;

► fazer reagrupamentos;

► fazer trocas;

► estimular o cálculo mental.

Para esta atividade, cada grupo deve ter um dado marcado de 4 a 9. Cada criança do grupo, na sua vez de jogar, lança o dado e retira para si a quantidade de cubinhos correspondente ao número que sair no dado.

Veja Bem: o número que sai no dado dá direito a retirar somente cubinhos.

Toda vez que uma criança juntar 10 cubinhos, ela deve trocar os 10 cubinhos por uma barra. E aí ela tem direito de jogar novamente.

Da mesma maneira, quando tiver 10 barrinhas, pode trocar as 10 barrinhas por uma placa e então jogar novamente.

O jogo termina, por exemplo, quando algum aluno consegue formar duas placas.  O professor então pergunta:

– Quem ganhou o jogo?

– Por quê?

Se houver dúvidas, fazer as “destrocas”.

O objetivo do jogo das trocas é a compreensão dos agrupamentos de dez em dez (dez unidades formam uma dezena, dez dezenas formam uma centena, etc.), característicos do sistema decimal.

A compreensão dos agrupamentos na base 10 é muito importante para o real entendimento das técnicas operatórias das operações fundamentais.

O fato de a troca ser premiada com o direito de jogar novamente aumenta a atenção da criança no jogo. Ao mesmo tempo, estimula seu cálculo mental. Ela começa a calcular mentalmente quanto falta para juntar 10, ou seja, quanto falta para que ela consiga fazer uma nova troca.

► cada placa será destrocada por 10 barras;

► cada barra será destrocada por 10 cubinhos.

Variações:

► Pode-se jogar com dois dados e o aluno pega tantos cubinhos quanto for a soma dos números que tirar dos dados.

► Pode-se utilizar também uma roleta indicando de 1 a 9.

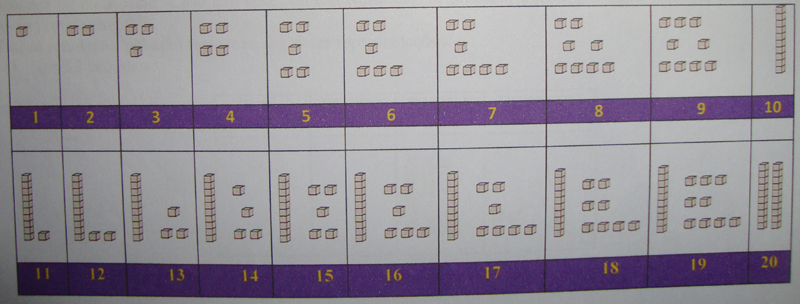
8) VAMOS FAZER UM TREM?

Objetivo: compreender que o sucessor é o que tem ” 1 a mais” na sequencia numérica.

O professor combina com os alunos:

– Vamos fazer um trem. O primeiro vagão é um cubinho. O vagão seguinte terá um cubinho a mais que o anterior e assim por diante. O último vagão será formado por duas barras.

Quando as crianças terminarem de montar o trem, recebem cartões nas quais devem escrever o código de cada vagão. Esta atividade leva à formação da ideia de sucessor. Fica claro para a criança o “mais um”, na sequencia dos números. Ela contribui também para a melhor compreensão do valor posicional dos algarismos na escrita dos números.

9) UM TREM ESPECIAL

Objetivo: compreender que o antecessor é o que tem “1 a menos” na sequencia numérica.

O professor combina com os alunos:

– Vamos fazer um trem especial. O primeiro vagão é formado por duas barras (desenha as barras na lousa). O vagão seguinte tem um cubo a menos e assim por diante. O último vagão será um cubinho.

Observação: idem ao exemplo da tabela acima, mas do maior ao menor número. Quando as crianças terminam de montar o trem, recebem cartões nas quais devem escrever o código de cada vagão. Esta atividade trabalha a ideia de antecessor. Fica claro para a criança o “menos um” na sequencia dos números. Ela contribui também para uma melhor compreensão do valor posicional dos algarismos na escrita dos números.

10) PREENCHENDO TABELAS

Agrupamentos e trocas na base 10

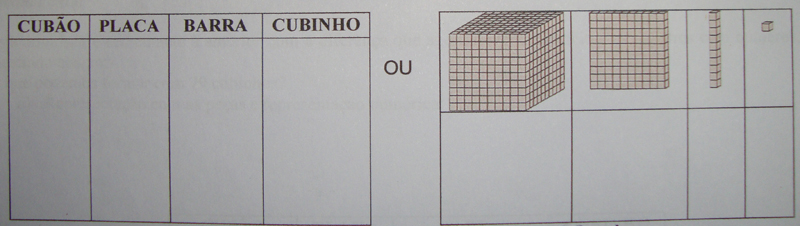
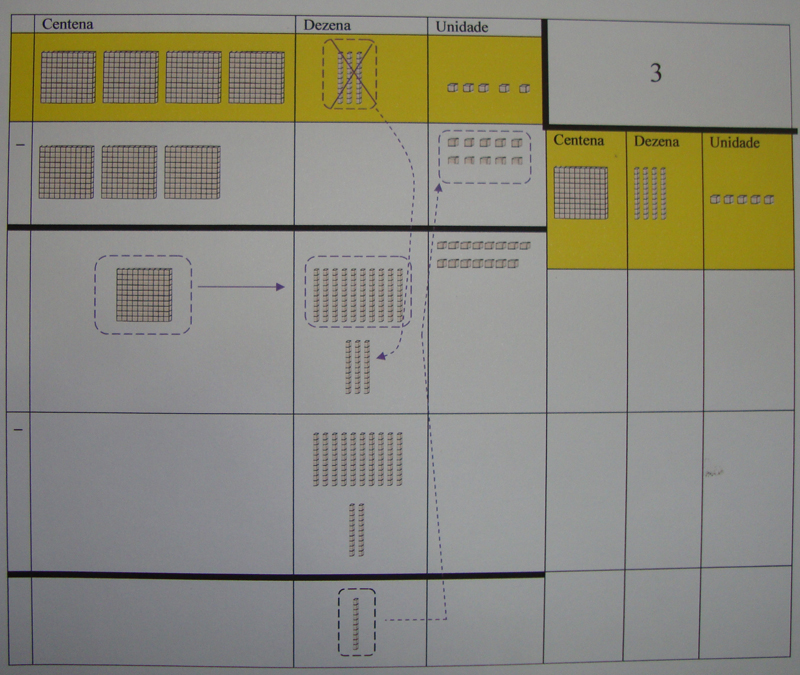
Nesta fase faz-se necessária a utilização de material de apoio, como um QVL (Quadro Valor de Lugar) que pode ter as formas apresentadas na Figura 4.

 Figura 4: Quadro valor de lugar para utilização do Material do Dourado

 

Objetivo: Estabelecer os padrões de agrupamento e desagrupamento, da mesma forma que fazemos com nosso sistema de numeração decimal, levando ao entendimento da construção da representação numérica neste sistema e auxiliando na compreensão futura das operações aritméticas.

Metodologia: O fundamental nesta fase é estabelecer a seguinte regra: nunca dez, ou seja, não podemos ter dentro de um mesmo espaço dez ou mais peças. Caso isto ocorra o estudante deverá proceder a troca por outra peça que deverá ocupar a próxima posição no QVL.

Assim, os estudantes poderão formar as seguintes representações:

a) com 32 cubinhos:

b) com 148 cubinhos:

 

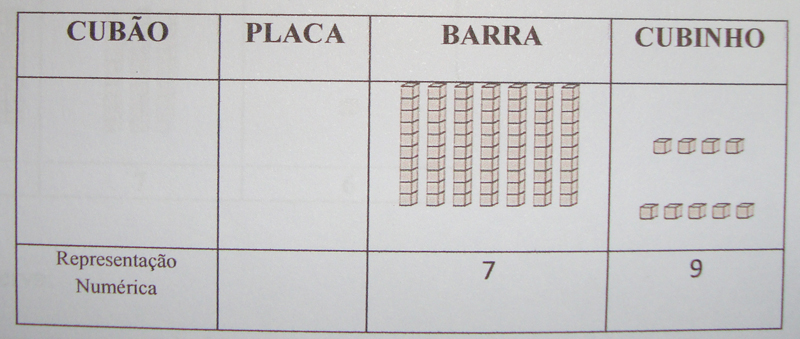
11) Representando agrupamentos e trocas

Objetivo: Fazer correspondência entre a representação com as peças do Material Dourado e a representação com signos numéricos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).

Metodologia: Esta atividade é semelhante à anterior com a diferença que agora deverão ser feitos os registros com números, como mostrado abaixo:

► O que podemos formar com 79 cubinhos?

a) Representação com as peças e representação numérica:

 

Operações matemáticas com o Material Dourado

Não há aqui a pretensão de colocar o Material Dourado como único recurso a ser trabalhado na construção de conceitos envolvendo as operações aritméticas. Sabe-se da importância da abordagem a partir de vários recursos e metodologias, bem como do longo caminho existente entre a utilização de materiais manipulativos para a realização das operações e a aprendizagem dos algoritmos e resolução de problemas. No entanto, haverá uma simplificação deste processo com o objetivo de destacar o potencial do Material Dourado como uma das ferramentas disponíveis na construção destes conhecimentos. Realizar operações matemáticas com o Material Dourado torna os processos mais fáceis de serem entendidos e aceitos por ser uma atividade prática e visual. O aluno pode se apropriar do conhecimento manipulando e verificando todas as fases dos vários processos de construção, podendo com isso assimilar, criticar e criar novas formas de organizar o seu pensamento, o que ajuda no desenvolvimento do raciocínio lógico-matemático. Várias são as operações possíveis de serem realizadas com este recurso, todas elas pressupõem o entendimento anterior das representações e das regras de agrupamentos e desagrupamentos. Algumas delas serão apresentadas a seguir.

 

Adição

A realização de adições com o Material Dourado deve ser feita com o auxílio do QVL. O ideal é que a evolução do grau de dificuldade ocorra gradativamente, inicialmente com adição sem reserva. O algoritmo da adição poderá ser compreendido facilmente se for introduzido paralelamente à realização das adições feitas com o Material Dourado. Como pré-requisito, os alunos devem dominar os conceitos e relações envolvendo o Sistema de Numeração Decimal.

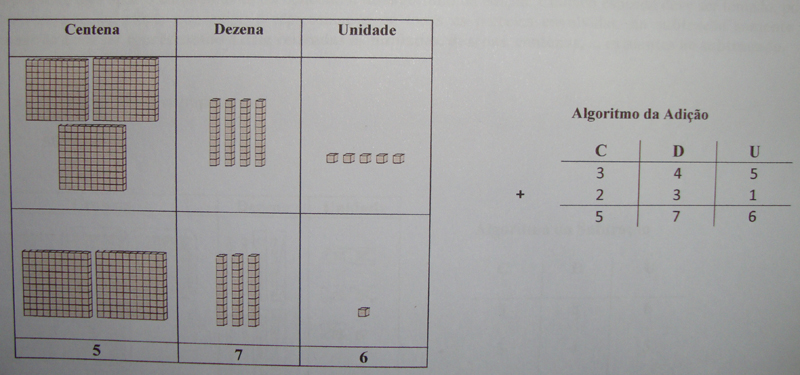
a) Adição sem reserva:

345 + 231

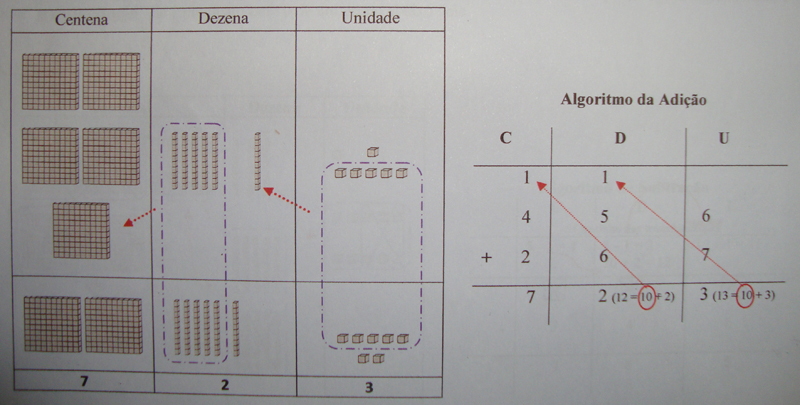
b) Adição com reserva:

É importante ressaltar que, com o uso do Material Dourado, fica claro para o aprendiz o processo do “vai um” como o agrupamento de 10 elementos, havendo, portanto, uma mudança no valor relativo do número, fica nítido que ocorre uma “transformação”.

456 + 267

 

Subtração

A realização de subtrações com o material dourado também deve ser feita com o auxílio do QVL com o mesmo cuidado no avanço gradativo de conceitos, iniciando com as subtrações sem desagrupamentos podendo ser realizadas em paralelo, mas após o entendimento do conceito e do algoritmo da adição. Cuidado especial deve ser tomado, pois diferentemente da adição que exige a representação de todas as parcelas envolvidas, na subtração somente o minuendo deve ser representado e dele retiradas as unidades, dezenas, centenas, … existentes no subtraendo.

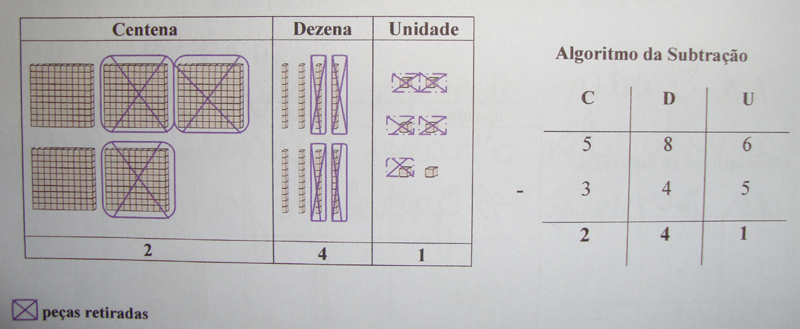
a) Subtração sem desegrupamento: 

586 – 345

 

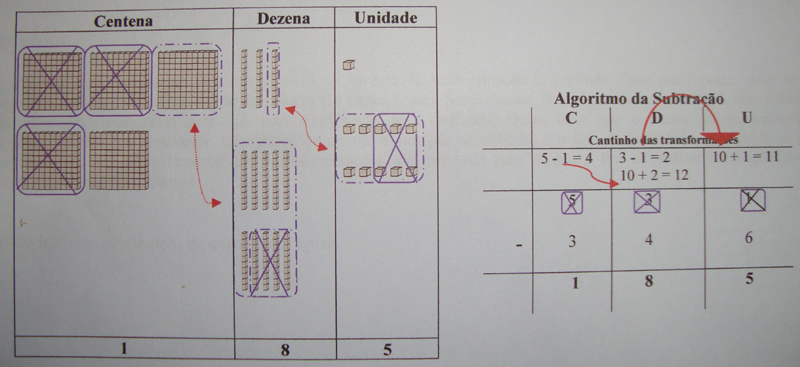
b) Subtração com desagrupamento:

Aqui o “pegar emprestado” ganha significado para o aprendiz (mas mesmo assim, evite usar essa palavra, sugerimos, transformar, trocar, etc.), pois ele passa a entender que há um desagrupamento e uma “transformação” de 1 elemento em 10 de um grupo abaixo dele.

531 – 346

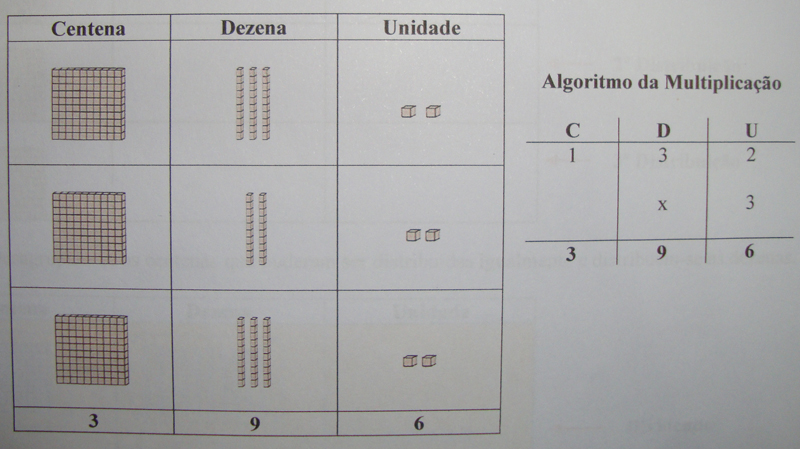
Multiplicação

Várias são as atividades que devem ser utilizadas para o entendimento do conceito da multiplicação, entre elas, a possibilidade da realização da multiplicação como adição de parcelas iguais. O algoritmo é a última escala neste processo que precisa ser entendido via conceituação de importantes propriedades: distributiva e comutativa, por exemplo. Tanto a multiplicação por adição de parcelas iguais quanto o entendimento do algoritmo da multiplicação podem ser facilmente aprendidos com o auxílio do Material Dourado, lembrando da importância da aprendizagem da tabuada como um dos fatores que influenciarão na fácil transposição entre todas as etapas.

a) Multiplicação como adição de parcelas iguais

3 x 132 = 132 + 132 + 132

 

Divisão

A divisão deve ser entendida como a operação inversa da multiplicação e, partindo deste pressuposto, deve ser considerada como uma distribuição de valores em partes iguais. Sendo assim, deve ser trabalhada no QVL com tantas partes quanto necessárias para que esta distribuição seja realizada. Outro fator que o aluno, no processo de aprendizagem, deve considerar, não obrigatoriamente e sim por descoberta, é o fato da facilidade conseguida se o processo se der, diferentemente das outras operações, da esquerda para direita a fim de melhor realização dos desagrupamentos necessários.

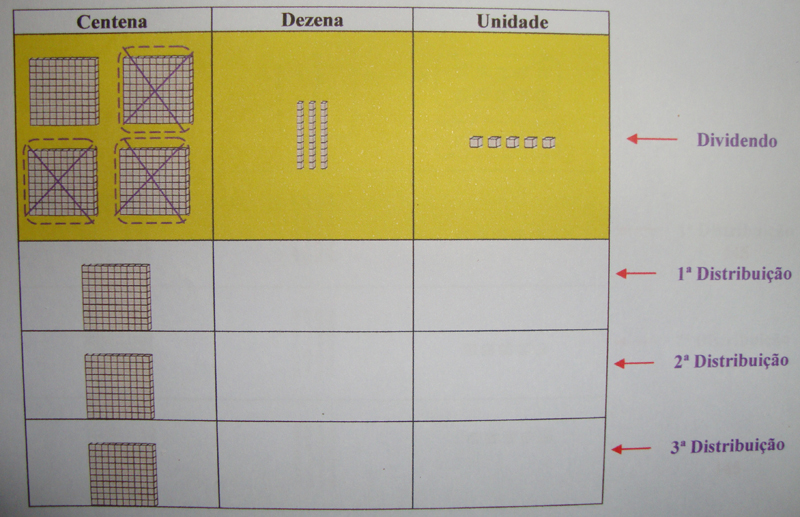
a) Divisão com distribuição de quantidades iguais

435 ÷ 3

► Primeiramente distribuem-se as centenas

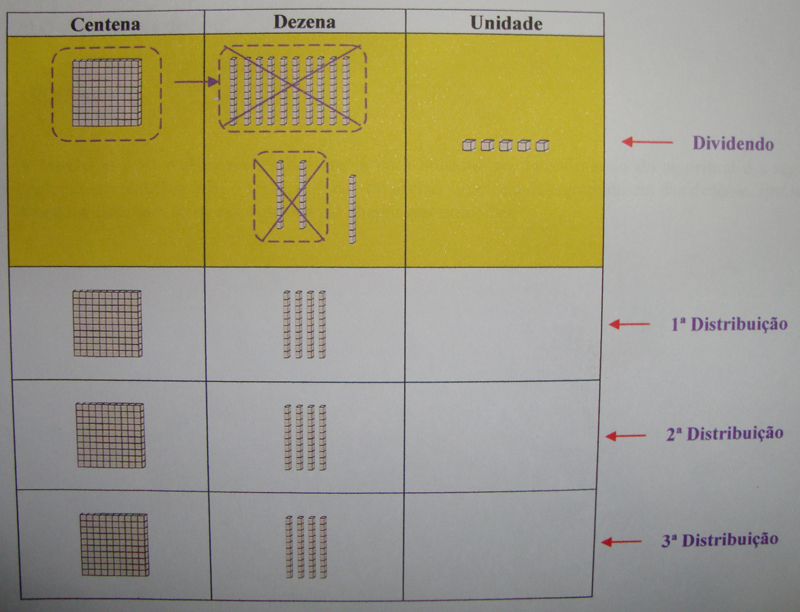
► Desagrupam-se as centenas que puderam ser distribuídas igualmente e distribuem-se as dezenas

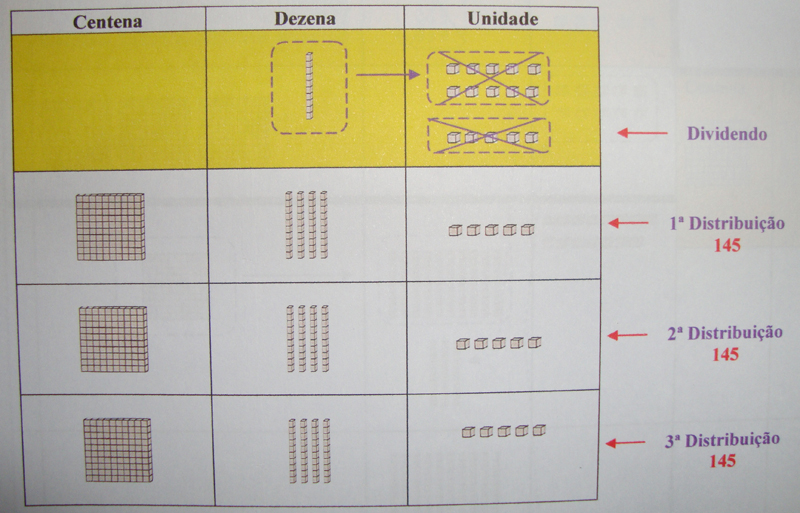
►Desagrupam-se as dezenas que puderam ser distribuídas igualmente e distribuem-se as unidades

b) O algoritmo da divisão

435 ÷ 3 

A estratégia para realização da divisão, já com enfoque no entendimento do algoritmo é a seguinte: dividem-se as centenas em partes iguais, o resto, que não dá divisão inteira é desagrupado em dez dezenas. Em seguida repete-se o procedimento para os demais grupos até chegar nas unidades.

BIBLIOGRAFIA

Centurión, Marília. Conteúdo e Metodologia da Matemática. São Paulo-SP: Editora Scipione, 1994.

Daltoé, Karen & Strelow, Sueli. Trabalhando com Material Dourado e Blocos Lógicos nas Séries Iniciais[2].

DANTE, Luiz Roberto. Didática da Matemática na Pré-Escola. São Paulo-SP: Editora Ática, 1996.

Freitas, Rony Cláudio de Oliveira. Um Ambiente para Operações Virtuais com o Material Dourado. Vitória – ES. Dissertação (Mestrado em Informática). Universidade Federal do Espírito Santo, 2004.

Pereira, Tânia Michel (Org). Matemática nas séries iniciais. Ijuí-RS: Editora UNIJUÍ, 1989.

Toledo, Marília & Toledo, Mauro. Didática de Matemática: como dois e dois: a construção da matemática. São Paulo-SP: FTD, 1997.

[1] A concepção de cooperação não é original do Método Montessoriano, que tem como maior crítica o incentivo à individualidade. Esta idéia foi incorporada recentemente após estudos, principalmente de pensadores como Piaget e Vygotsky.

[2] Disponível em: http://www.somatematica.com.br>. Acesso em: 13 de junho de 2010.