Logo após, mostrei a figura do triângulo. Conversamos sobre ele. Os tipos de triângulos: equilátero, isósceles, escalenos e os triângulos retângulos. Mostrei cada um deles com palitos de churrasquinho e garrote. Foi então, que tentei balançar um dos triângulos e eles perceberam que não se mexia. Peguei os demais e também fiz o mesmo procedimento, e eles repararam que os triângulos não tinham o movimento que o quadrado e o retângulo tinham. Perguntei aos surdos porque isso acontecia. Tentaram me explicar mas não foram muito convincentes. Dei as figuras para que eles percebessem tatilmente a rigidez do triângulo e a fragilidade do quadrado e do retângulo.  Eles testaram cada figura novamente: o quadrado, o retângulo e os vários tipos de triângulos. Então, expliquei que o triângulo é a figura mais rígida que existe. E que por essa propriedade característica do triângulo faz com que ele seja bastante usado nas construções e muito utilizado na praticidade de nosso dia a dia. Foi nesse momento que mostrei um quadrado e um retângulo com uma de suas diagonais definidas com outro palito de churrasco. Balancei a figura e conseguiram entender que essa diagonal dividiu o quadrado e o retângulo em dois triângulos e por isso, eles ficaram mais rígidos.

Foram mostradas as fragilidades em outras figuras, para que os alunos esclarecessem bem suas dúvidas e percebessem o que se estava discutindo. Com o uso do material, se percebeu uma rápida compreensão e um entendimento claro da importância da “dureza” do triângulo no cotidiano e também ficou claro da sua grande vantagem na possibilidade de seu uso.

Mostrei também que quanto mais triângulos colocarmos nas figuras mais rígida ela fica. Observe:

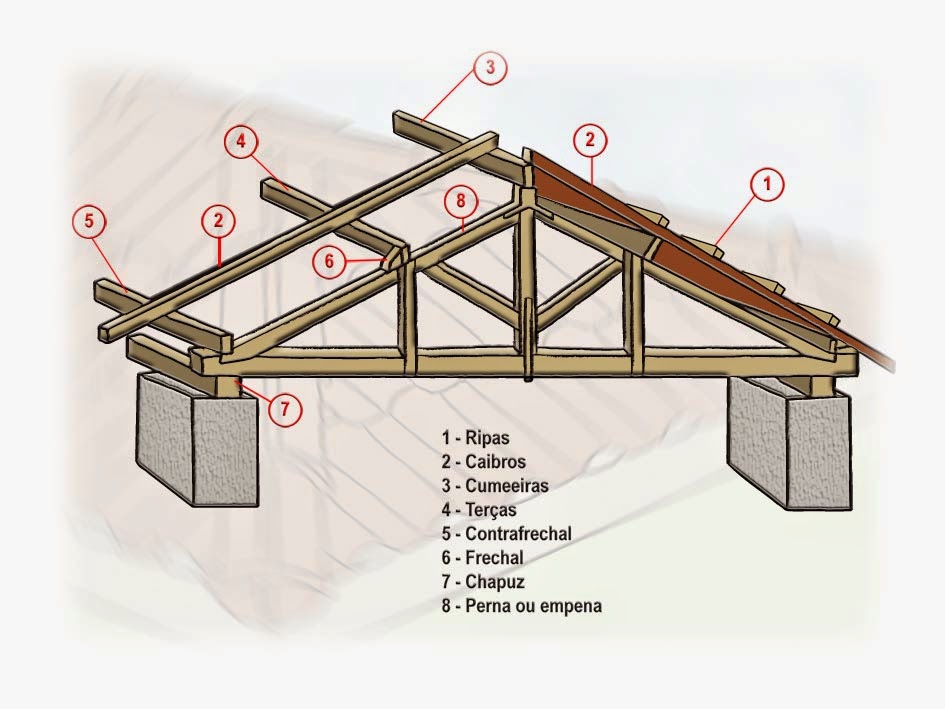
Levei o computador e mostrei algumas imagens que demonstram a aplicabilidade dessa propriedade dos triângulos em nosso cotidiano assim concretizando esse conceito.

24/03/2014
Neste dia levei papel pardo, fita métrica, régua e pincel atômico. Devido a forte chuva nessa noite, havia apenas dois alunos surdos na sala de aula. Propus para eles a construção de um quadrado, mas agora não com palitos de churrasquinho e sim, usando o papel pardo. Esse quadrado deveria ter 1 metro de lado. Confusos, os alunos construíram o quadrado com minha ajuda. Fiquei de retomar a construção feita na próxima aula com todos os alunos presentes.

31/03/2014 e 07/04/2014
Nestes dois dias de encontro pedi para eles fazerem algumas figuras usando os palitos de churrasco e garrote. Cada um fez a figura que quis, sendo que alguns destacaram algumas diagonais para deixar a figura mais rígida. Retomei  no dia 07/04 o quadrado feito de papel pardo, pois no dia da construção não estavam todos os alunos. Falei da importância do quadrado e o que significava esse quadrado contendo 1 m de largura e 1 m de comprimento (1 m x 1 m). Interroguei o grupo para saber se tinham alguma noção do que significava a palavra ÁREA  e como encontrávamos, por exemplo, a ÁREA da sala de aula usando aquele quadrado. Alguns alunos ficaram com dúvidas, deu para perceber que não relacionavam ou tinham tido pouco ou nenhum contato mais concreto com esse assunto. Não estou querendo dizer que não tenham estudado ÁREAS, mas acredito que tenham visto mais abstratamente, dificultando a relação teoria/prática/vivências. Como um deles trabalha na construção de móveis em MDF, me ajudou muito na explicação. Eu sempre que posso me aproveito dos saberes que algum aluno possa ter, pois me ajuda no aprofundamento da explicação. 

Explico melhor: sou professor ouvinte e domino a Língua de Sinais, mas acredito que um surdo usando sua língua mãe, facilita muito a compreensão do que se está falando. Através de algum exemplo, o aluno surdo que dominava o assunto, ajudo muito nas experiências vivenciadas por ele e relacionando-a com o conteúdo abordado. Foi o que aconteceu. Esse aluno, trabalha diretamente com madeira, cortando, encontrando o valor dos lados das placas de madeira, seus perímetros, áreas, etc. Foi com esses saberes que junto com o aluno explicamos então, como encontrar a ÁREA  da sala de aula. Afastei algumas classes e cadeiras e fui colocando o quadrado de papel pardo de 1 m x 1 m lado a lado, preenchendo o chão da sala. Fomos contando quantos quadrados desses cabiam na sala. Fomos para o quadro e representamos numericamente o que encontramos. Levei fita métrica e medimos o comprimento da sala e sua largura. Representamos também isso numericamente no quadro. 

Mostrei que se multiplicássemos esses dois valores iriamos encontrar também quantos quadrados cabiam na sala. Numericamente, encontramos valores bem aproximados, até porque a medição foi um pouco “grosseira”. O aluno surdo que estava me ajudando inclusive, fez referência as lajotas que costumamos comprar em lojas de construção para azulejar pisos ou paredes de nossa casa ou em outros lugares. Foi bem cansativo toda essa explicação, demoramos muito, explicando, voltando a explicar, dando muitos exemplos, relacionando muito com o cotidiano deles. Nesses exemplos então, aproveitamos para mostrar o que significava a escrita m². E relacionamos com o quadrado feito de papel pardo: 1 m x 1 m = 1 m². Confesso que me senti agraciado e recompensado por tanto esforço na explicação e agradeci ao aluno surdo pela ajuda. Acho super válido aproveitar o conhecimento e o domínio da língua para aprofundar conceitos que, muitas vezes, ficam muito abstratos e sem compreensão. 

Depois disso, reforcei a utilidade das figuras por eles construídas. Tive a ideia de sobrepor as figuras feitas nas janelas da sala, na classe, na porta, nas paredes e nos murais e em todas as coisas que pudéssemos relacionar, para que notassem a presença constante delas em nosso dia a dia. Faço isso porque temos surdos que tem outros comprometimentos e precisamos reforçar bastante para que haja uma compreensão e um entendimento no que estamos falando e principalmente entender o conceito matemático envolvido.  

Primeiramente, coloquei as figuras feitas com palitos de churrasquinho e retomei as propriedades de cada figura. Levei para sala de aula uma sacola de caixas de remédios, de perfumes e etc. Peguei uma das caixas e coloquei na minha mesa. Era uma caixa de pasta de dente. Posicionei a caixa conforme a posição da sala de aula e expliquei que a caixa representaria nossa sala. Destaquei as paredes da sala referenciando-os aos lados da caixa. 

Fiz alguns questionamentos: A parede que tem as janelas corresponde a que lado da caixa? A parede que está o mural azul corresponde a que lado da caixa? O teto da sala de aula corresponde a que face da caixa? E o chão da sala de aula? Com isso consegui que eles transportassem os lados da sala (paredes, teto e chão) para as faces da caixa que estava representando a sala. Isso facilitou muito o entendimento e a inter-relação entre concreto e o abstrato. Ajudando na conceituação teórica do conteúdo.