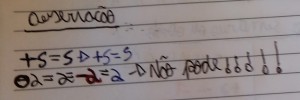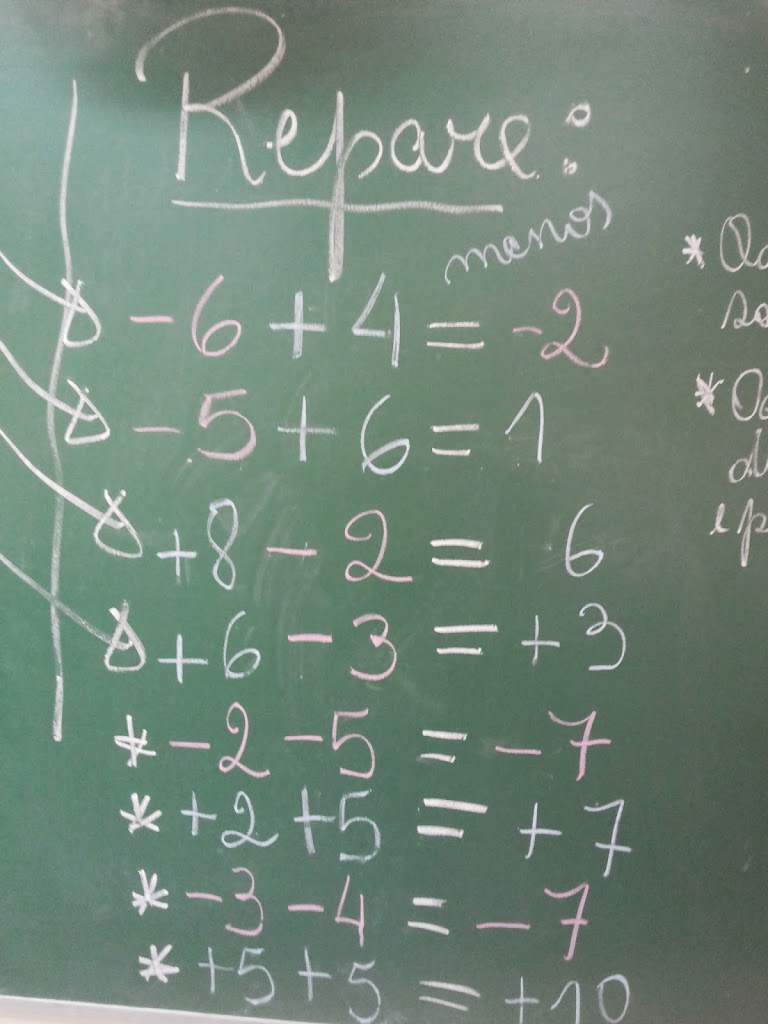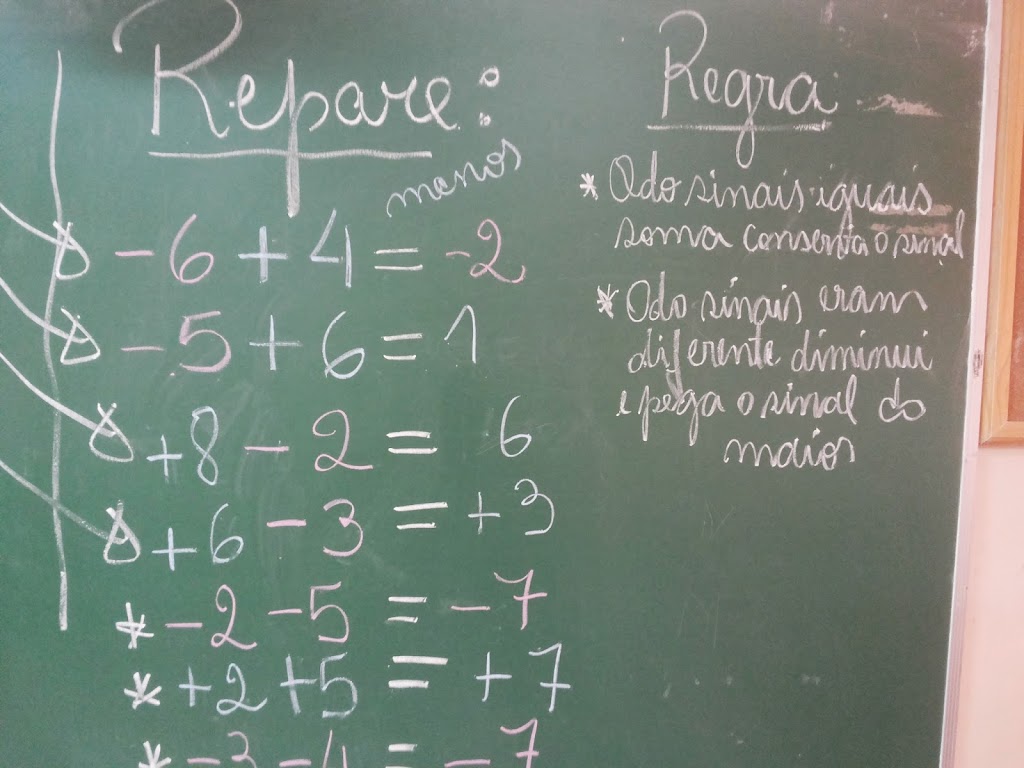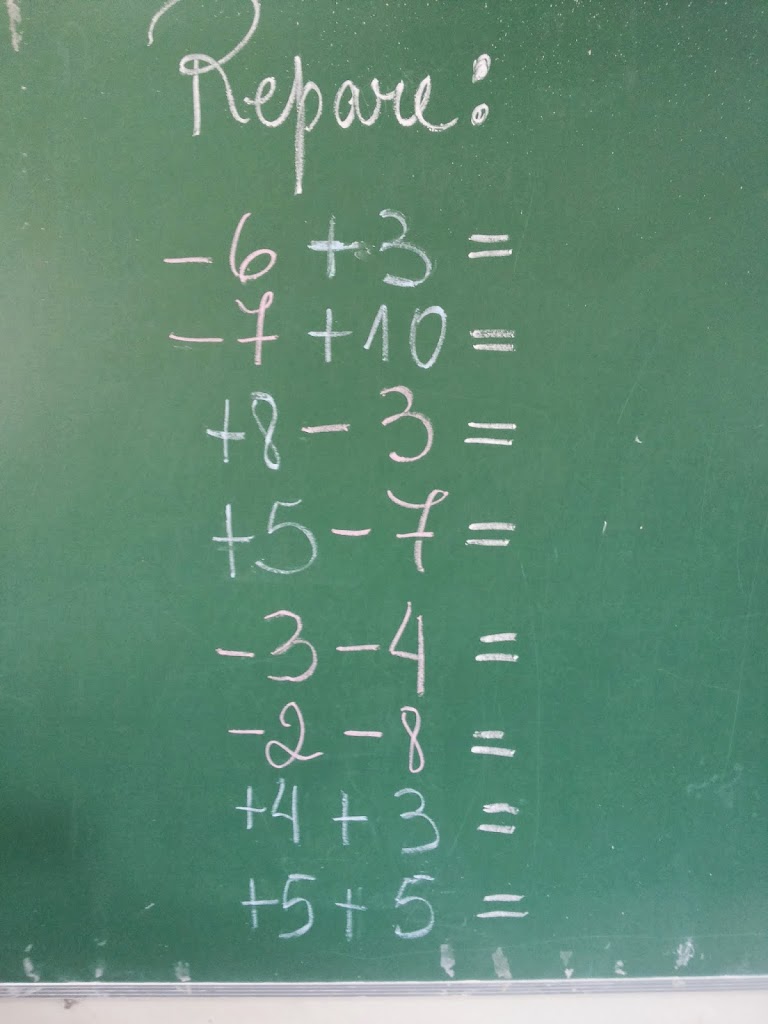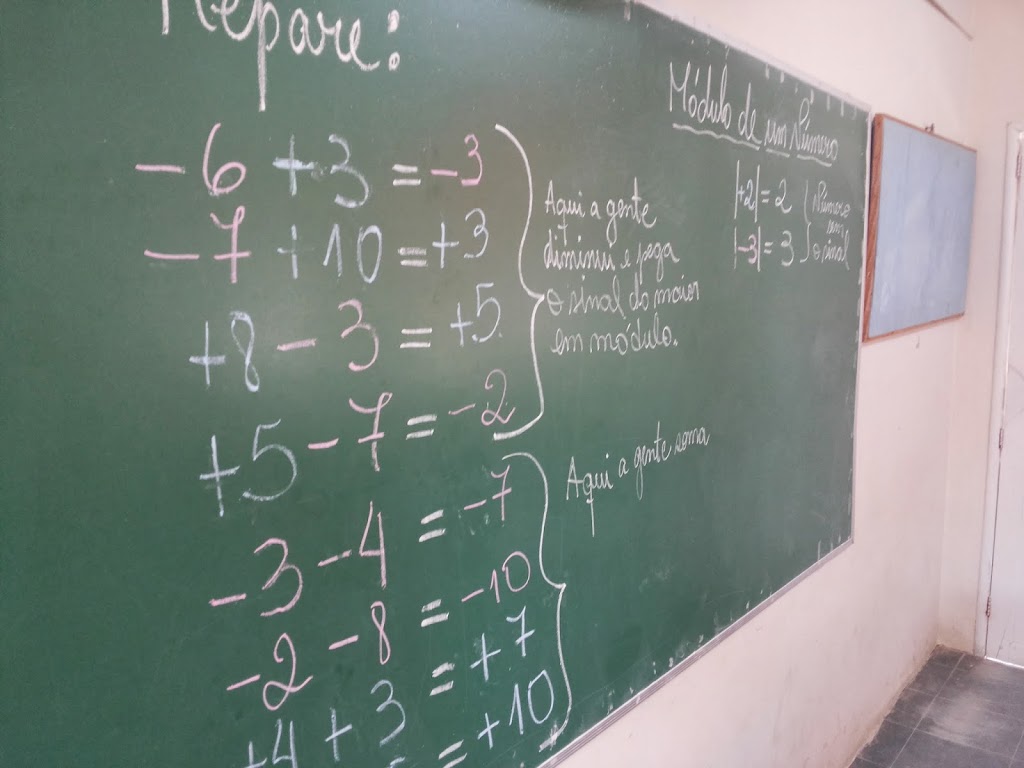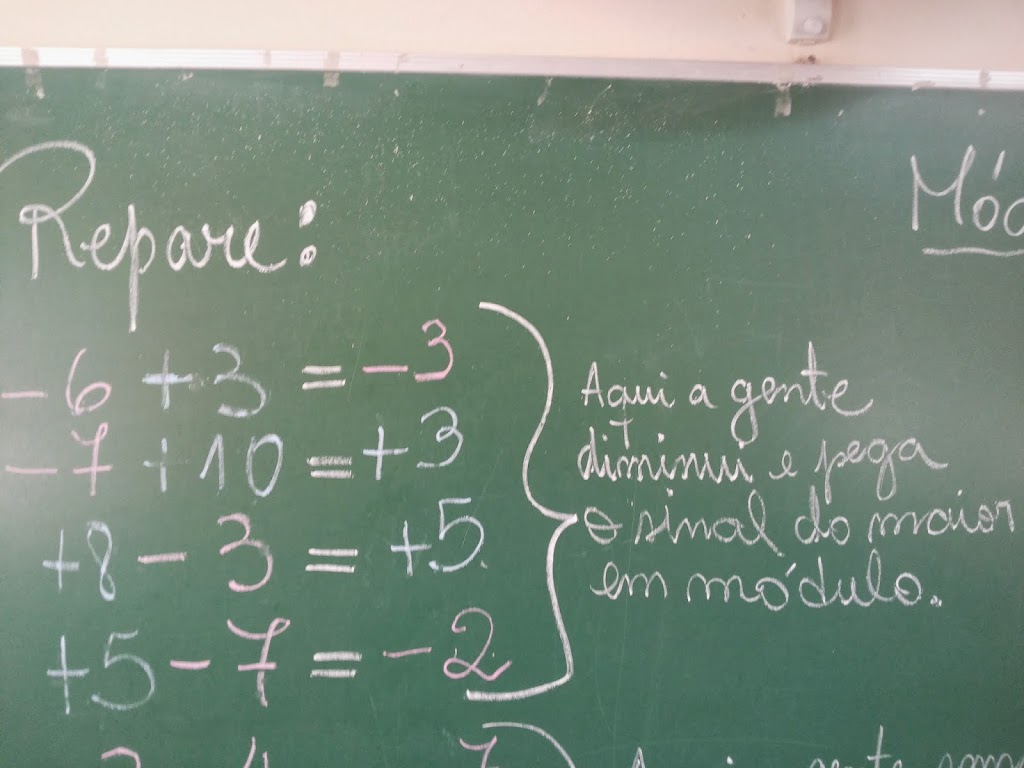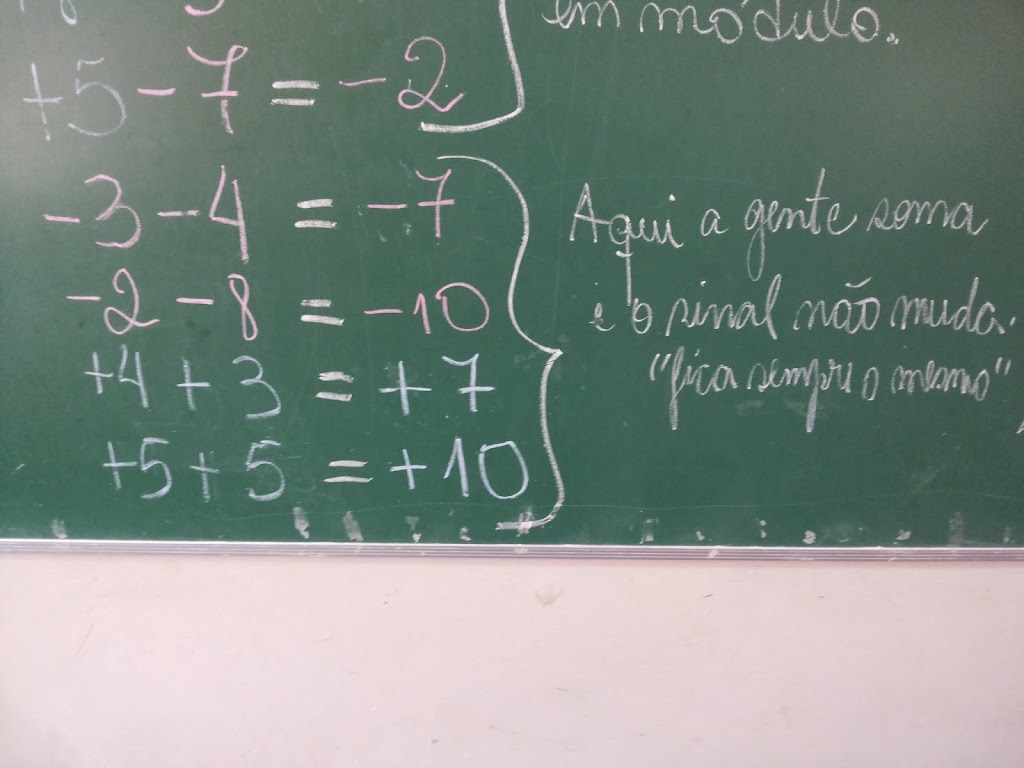20/03/2014
Neste ano (2014), estou lecionando, na Escola Municipal de Ensino Fundamental Ministro Arthur de Souza Costa, na 6ª e 8ª série. Geralmente, na 6ª série, costumo introduzir a ideia de Número Positivo e Número Negativo utilizando fichas coloridas.
Antes disso, retomo o Conjunto dos Números Naturais. Digo para eles que nos anos iniciais até a 4ª série, utilizaram bastante esse conjunto. Principalmente, as 4 operações básicas. Lógico que eles já tiveram contato com o Conjunto dos Números Racionais, mas nesse momento não cito esse conjunto, pois depois estaremos estudando ele especificamente.
Mas, tento retomar os Números Naturais salientando que durante o transcorrer da história da civilização humana, conforme Imenes (Coleção Pra que serve Matemática?, Ed. Atual, 1992), o homem necessitou registrar outros tipos de números além dos que já conhecia.
Segundo Imenes, o Número Negativo teria surgido para representar a retirada de peças de caixas por funcionários estocadas em portos. Diz ele, que funcionários de Armazéns de portos quando retiravam, por exemplo, 2 peças da caixa, escreveriam: minus 2 (Latim minus = menor, mais pequeno), ou quando havia excesso de peças na caixa, por exemplo, escreveriam: plus 3 (Latim plus = mais). Com o tempo, minus teria sido abreviado para m, conta Imenes. E que devido a correria do dia a dia, o m teria sido substituído pelo sinal ” – “.
A mesma coisa com a palavra plus. No decorrer do tempo, teria sido substituída pelo sinal “+“. Imenes salienta que mesmo essa história do surgimento dos números positivos e negativos poderia ser uma lenda, e que provavelmente esses sinais teriam surgido da necessidade do homem em seu cotidiano de simbolizar numericamente o excesso ou a falta de alguma coisa. Assim, vou demonstrando o surgimento desse outro número: O NEGATIVO.
Dessa forma, demonstro que o homem também necessitou reorganizar esses números novos que iam surgindo. Desta forma, o CONJUNTO DOS NÚMEROS INTERIOS veio para ampliar possibilidades de operações e resolver inúmeros “entraves” científicos e tecnológicos. Tento também explicar que na matemática usa-se representar ou homenagear contribuições dos povos nessa ciência. Gregos, Egípcios, Franceses, Indus, Árabes e Alemães e tantos outros que contribuíram para o desenvolvimento da Matemática.
Por isso, neste caso, temos a letra Z representando o CONJUNTO DOS NÚMEROS INTEIROS, isso porque ZAHL em alemão significa NÚMERO. Uma das homenagens aos alemães à contribuição da Matemática.
Primeiramente, mostro como fica esse novo conjunto. Que representamos para a direita do zero os números naturais que chamaremos de positivos. E para a esquerda do zero nosso novo número negativo.
Z = {…, -5, -4. -3, -2, -1, 0, +1, +2, + 3, +4, + 5, … }
Além de salientar que o número zero não terá sinal, pois é neutro, reafirmo que o conjunto é infinito para a direta (positivo) e para a esquerda (negativo). E pergunto uma coisa para os alunos: Se uma coisa é infinita, como por exemplo o céu, existe o meio? Sempre fiquei indignado quando as crianças me respondem que o zero fica no meio do conjunto ou no meio da reta. Tento deixar isso bem claro para eles.

Peço que usem uma régua e tracem uma reta. Depois que marquem numa mesma distância ( 1 cm ) pontos nela. É ai que saliento uma coisa importante. Digo para eles que o professor quer representar números positivos e negativos na reta, por isso que neste caso temos a impressão que o zero fica no meio. Mas isso não é sempre assim. Pois em alguns momentos posso querer representar mais números negativos ou números positivos e por falta de espaço salientamos mais um lado do que o outro. Então não teremos aquela visão da reta que nos remete que o zero está no meio. Destaco também a distância entre os números. Nesse momento também questiono algumas coisas comparando os números. Para que eles percebam que quanto mais longe a direita do zero estiver, o número, maior ele é. Quanto mais longe a esquerda do zero estiver, o número, menor ele é. Ai faço algumas perguntas como: quem é maior, o + 9 ou – 7? O – 10 ou + 20? O – 50 ou + 10? O – 30 ou – 11? O + 100 ou + 150? O – 100 ou + 1? E assim por diante.
Esclareço que dependendo da necessidade, a distância pode ser 2 cm, 3 cm, 4 m, mas que entre um número e o outro a distância deverá ser sempre igual. Nunca poderão marcar o + 1 distante de 1 cm do 0 e o + 2 distante 4 cm do 0, e assim por diante.
PESSOAL, QUERO DEIXAR CLARO QUE ESTE É MEU PLANEJAMENTO DE AULA. É ASSIM QUE TENTO EXPLICAR TODA A CONSTRUÇÃO DA IDEIA DE NÚMERO POSITIVO, NEGATIVO, SEU SURGIMENTO NA HISTÓRIA E SUA REPRESENTAÇÃO GRÁFICA NA RETA.
Outra coisa que destaco antes de começar a operar com Números Inteiros é explicar o que são NÚMEROS SIMÉTRICOS ou NÚMEROS OPOSTOS. Aproveito que estou explicando a distância em que os números devem ser colocados na reta e saliento o que são números opostos. Mas, também faço uso das fichas para mostrar que um número oposto ao outro ZERA, ANULA. Demonstro que se pegarmos o número + 4, seu oposto é – 4 e saliento que a distância com referência ao ZERO é a mesma. Cito outro números como exemplo para verificar se entenderam.
Como falei acima, demonstro também usando as fichas. Mostro que se eu tenho uma ficha azul e juntar com uma vermelha elas vão se ANULAR, ZERAR. Se eu tenho duas fichas azuis e juntar duas fichas vermelhas também se irão anular. Levo as fichas e mostro na reta no quadro onde elas estariam situadas e demonstro que a distância com referência ao zero, é a mesma.
É incrível, não preciso muito esforço para que os alunos percebam isso rapidinho. As fichas funcionam muito bem!!!
Aqui estão os potes que uso para trabalhar os Números Inteiros. Deixo a disposição dos alunos para que eles manuseiem se necessário. Forneço um punhado de fichas para que em algumas atividades eles possam usar e concretamente possam aplicar o que vou explicando. Eles tentam executar o que falo, principalmente alguns alunos que demonstram mais dificuldades. Mas percebo que com o uso das fichas, essas dificuldades são esclarecidas rapidamente.
Os potes com as fichas azuis e vermelhas
Aluna pegando fichas para verificar números opostos
Peço também que eles tragam de casa ou eu mesmo forneço, lápis de cor AZUL e VERMELHO. Combino com eles que vamos estar representando, num certo momento, as descobertas que vamos fazendo com esses números novos. Realizo algumas atividades para que eles se apropriem da ideia de NÚMERO POSITIVO, NÚMERO NEGATIVO e NÚMEROS OPOSTOS, usando os lápis de cor.
Por exemplo, usando os lápis de cor e as fichas, peço que escrevam:
+ 5 – 3 = pegam 5 fichas azuis e 3 vermelhas e fazem a combinação de números opostos.
+ 9 – 4 = pegam 9 fichas azuis e 4 vermelhas e fazem a combinação de números opostos.
REPAREM NAS FOTOS:
Fazendo os cálculos com as fichas e
registrando no caderno com a cor encontrada
Fazendo os cálculos com as fichas
Fazendo o cálculo com a fichas
Fazendo os cálculos com as fichas e
combinando os simétricos para encontrar o resultado
Fazendo os cálculos com as fichas e
combinando os simétricos para encontrar o resultado
Fichas combinadas
registrando o resultado encontrado com a cor correspondente
Neste momento faço uma ressalva muito importante. Pego o giz colorido (azule vermelho) e as fichas e faço um esquema demonstrando algo primordial que muitas vezes leva ao erro.
Peço que anotem também no caderno:
+ 5 = 5
5 fichas azuis se não colocar o sinal continuam 5 fichas azuis
(VERDADEIRO)
– 2 = 2
2 fichas vermelhas se não colocar o sinal, se transformam em duas fichas azuis
(FALSO)
Aqui, anotação de um aluno salientando que nesse segundo exemplo, se esquecermos o sinal de NEGATIVO DO NÚMERO (ficha vermelha). ele “vira” ficha AZUL, isto é, UM NÚMEROPOSITIVO. Portanto, isso NÃO PODE ACONTECER!!!!
Isso fica bem claro para os alunos, percebem como é diferente, como modifica a resposta, pois modifica a cor.
Os registros continuam no desenvolvimento da explicação, sempre usando os lápis de cor, inclusive, podem observar no caderno do alunos, as respostas das atividades fornecidas por mim também são coloridas conforme o resultado das fichas.
Alunos tentando encontrar as respostas dos exercícios fornecidos, utilizando as fichas coloridas e os lápis de cor. É impressionante a rapidez da compreensão do que é um NÚMERO POSITIVO e um NÚMERO NEGATIVO utilizando esse recurso. Facilita muito a compreensão e principalmente, o entendimento da importância de não esquecer o sinal correspondente ao número que encontramos. Claro, que eles sabem que o número azul podem deixar sem o sinal. Mas eles mesmos fazem questão de colocar. E se eu não coloco no quadro, me chamam a atenção. Mas, aos poucos quero ir demonstrando que em certos momentos não há necessidade de colocar e também que eles percebam abstratamente que o número continua positivo.

Na semana passada, em uma das turmas, chegou o momento de concluirmos algumas coisas, devido a rapidez que eles estão assimilando o conceito de número positivoe negativo. Então fiz uma relação de operações com o propósito de eles mesmos concluírem algumas coisas sobre o que acontece quando operamos esses número.
REPARE, EU NÃO DEI REGRAS DE SINAIS ATÉ AGORA. A REGRA DE SINAIS QUE ESTÁ AO LADO DOS EXEMPLOS FORAM ELES MESMOS QUE CONSTRUÍRAM, NÃO FOI FORNECIDA POR MIM.
Não está muito nítido nas fotos, devido ao giz ser muito claro. Mas vou descrever melhor aqui o que foi feito. Eles já tem a noção de Módulo de um Número pois foi referido anteriormente quando trabalhei a comparação entre eles. Então, escrevo (sem colocar a resposta, vamos fazer isso juntos e usando as fichas para poder concluir):
REPARE:
1º) -6 + 4 = – 2
2º) –5 + 6 = + 1
3º)+8 – 2 = 6
4º)+6 – 3 = + 3
5º) -2 – 5 = – 7
6º)+2 + 5 = + 7
7º)-3 – 4 = – 7
8º)+5 + 5 = + 10
Com esses dados, os alunos conseguem comparar com o que está sendo dito. Acabam percebendo e eles próprios descrevem o que está acontecendo usando suas próprias palavras e conclusões. Do 1º ao 4º exemplo eles percebem que devem diminuir porque estão trabalhando com as duas cores de fichas (azul e vermelho) e que precisam combinar para eliminá-las, assim, saber que ficha e que cor sobra. Mas, ao mesmo tempo, se dão conta que tendo-se mais fichas vermelhas queazuiso resultado será vermelho ou, tendo-se mais fichas azuis que vermelhas, o resultado será azul. E que o que “manda” é a COR DO NÚMERO MAIOR EM MÓDULO.

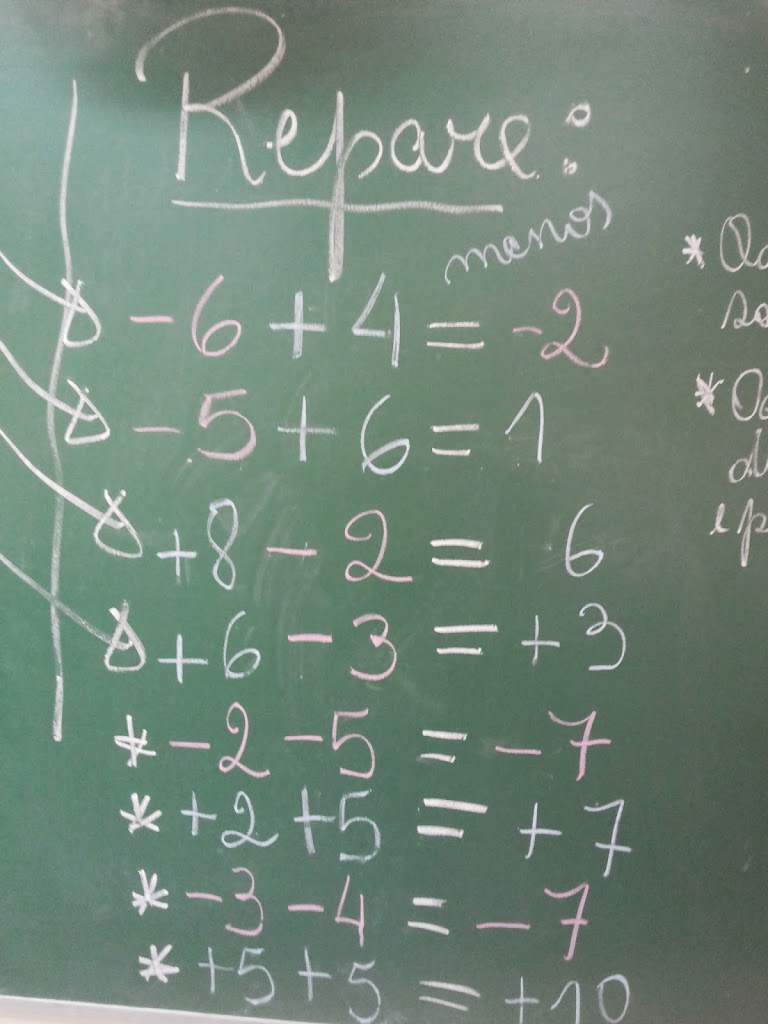
Eles mesmos construíram a REGRA DE SINAIS, apenas anotei a conclusão deles. Esta semana estarei reforçando o que acontece quando temos sinais diferentes e sinais iguais envolvidos numa operação. Mas, em nenhum momento darei ênfase a REGRA. Também não pretendo fazer CARTAZ COM A REGRA DE SINAIS. Pretendo que eles memorizem lembrando da cor: quando ela difere e quando são iguais numa operação e o que deverá acontecer, que ficha resulta e que cor. Estarei anotando e divulgando a apropriação desse processo por aqui.
24/03/2014
Hoje reforcei bastante nas duas turmas o que acontece com os sinais quando operamos cores diferentes ou cores iguais. Recoloquei as operações novamente no quadro, mas refiz cada operação com o uso das fichas e separei as quatro primeiras em uma mesa e as quatro últimas em outra mesa. Tudo isso, para que eles percebessem bem o que acontece em cada caso.
Refizemos os cálculos e separei as operações em dois blocos no quadro. Retomei a ideia do MÓDULO DE UM NÚMERO, pois queria que eles comparassem o que acontece quando os sinais são diferentes de forma tranquila sem decorar nada, apenas concluindo.
Reparem que foi colocado no quadro exatamente o que eles iam dizendo, como: “Aqui a gente diminui e pega o sinal do maior em módulo“. “Aqui a gente soma e o sinal não muda, fica sempre o mesmo“. Conclusão deles mesmos.
Ao mesmo tempo que íamos fazendo as operações acima, eu ia realizando com o uso das fichas, os cálculos. Resolvi separar em duas mesas. A primeira mesa à direita, está o primeiro bloco de cálculos: USA-SE AS DUAS CORES DE FICHAS: AZUL E VERMELHO. Lembrei que sempre que combinamos uma ficha azul com uma vermelha ANULA, ZERA.
Assim, realizamos cada operação. Repare na mesa à direita: – 6 (seis fichas vermelhas) e+3 (três fichas azuis). As azuis foram sobrepostas acima das vermelhas sem cobri-las totalmente para perceberem a “anulação” dos números opostos. Desta forma também, o aluno consegue ver a quantidade de ficha que corresponde ao número maior em módulo e sua cor.
A cada passo e resolução simultânea no quadro, era relembrado: Por que diminuímos? Que cor sobrou a mais? Qual é a sua quantidade em módulo?
No segundo bloco, na mesa à esquerda, está as operações que envolveram números com o mesmo sinal, isto é, com a mesma cor. Várias vezes perguntei: temos fichas para COMBINAR e ANULAR? As fichas, por exemplo, – 3 (três fichas vermelhas) e – 4 (quatro fichas vermelhas), podemos combinar e anular? NÃO, POIS SÃO IGUAIS NA COR! Então, somamos as fichas para saber quantas temos. E assim por diante. Foi feita a mesma coisa para os outros três exemplos.
Mesa com as operações que envolviam cores iguais. Questionei, perguntei e retomei várias vezes para eles perceberem que quando as cores são iguais (os sinais são iguais), somamos. E perguntava: e a cor? E o sinais, como ficam? Continua o mesmo, professor. Respondiam rapidamente e em coro.
Mesa com as operações que envolviam cores diferentes. Aqui novamente, perguntei, questionei e retomei várias vezes o que estava acontecendo. Pedia que analisassem bem o que sobrava em cada operação (ficha) e qual a relação com o MÓDULO DE UM NÚMERO. Tudo isso para que eles mesmos percebessem sem levá-los a decorar nada. Só concluindo.
Realizei pequenas atividades para ver como estavam interpretando e assimilando as operações com os número inteiros. Achei interessante como alguns alunos registravam usando lápis colorido a resposta positiva ou negativa. Isso me levou a crer, que utilizando esse tipo de material, facilita muito a compreensão sem necessitar de regras que intimidam e pressionam o aluno a decorar sem entender muitas vezes o que está acontecendo.
Nessa outra turma, a aluna refrizou: “quando são diferentes professor, diminui e pega o sinal do maior em módulo“. E “quando são iguais os número FICA O MESMO“. Claro, que ela quis dizer que “fica o mesmo sinal”. Mas, escrevi conforme ela falou, e escrevi com uma letra maior, pois eles já tinham visto isso na aula anterior e eu apenas estava recapitulando.




Fiquei muito satisfeito com o resultado. Falei hoje, que aos poucos vou retirando as cores e que precisaríamos ir memorizando as conclusões feitas. Também fizemos exercícios envolvendo parênteses usando entre os parênteses sinais de + e sinais de – . E inacreditavelmente, me impressionou a rapidez que compreenderam tudo. Lógico, que tenho alguns alunos com mais dificuldades, inclusive repetentes. Mas pouquíssimas dúvidas surgiram, pediam mais e mais exercícios. Reparei que não faziam as atividades com má vontade, pelo contrário, assumiam a atividade como um desafio e ansiosamente queriam resolver e disputavam entre eles quem resolvia mais rápido. Continuo dizendo: NAO VOU USAR CARTAZ COM REGRA DE SINAIS. Só quando entrar com a multiplicação e a divisão de números inteiros. Se achar que é necessário, farei um esquema e anexarei na sala. Já que as operações envolvendo sinais na multiplicação e na divisão é mais difícil de explicar e mostrar porquê isso acontece.