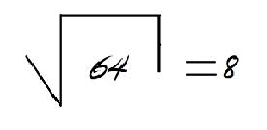POTENCIAÇÃO
Autor: JFDuran
Em 2013 lecionei para a 5ª série na Escola Municipal de Ensino Fundamental Ministro Arthur de Souza Costa. No 1º trimestre trabalhei com o conteúdo de Potenciação e Radiciação. Resolvi fazer um planejamento bem dinâmico, no qual os alunos pudessem participar ativamente na construção da ideia de Potenciação e de Radiciação. Fiz várias cópias de uma folha de ofício quadriculada 1cm x 1 cm, forneci uma cópia para cada aluno. Já tinha feito esse trabalho quando lecionei na Escola Estadual N. Sra. de Fátima no bairro Cohab – Fragata/1993. Naquela época, o CERENEPE de Pelotas, construía muitos materiais em madeira, jogos, etc. Tinham uma loja no próprio prédio em que vendiam esses materiais e faziam encomendas. Então, resolvi ir até lá e encomendei 64 cubos em madeira com arestas 4cm: 16 vermelhos e o resto de cor amarela. Para facilitar o transporte pedi também que acomodassem todos eles dentro de uma caixa/cubo com tampa deslizante. Aproveitei a ida e visitei a oficina e os alunos que trabalhavam nela. Fantástico o empenho e a dedicação!
Voltando ao planejamento atual, digo para os alunos que vamos construir muros. Esses muros terão uma particularidade: serão quadrados. Vou separar por momentos a explicação para facilitar melhor o transcorrer da ideia.
1º MOMENTO:
Digo para os alunos que vamos construir muros. Esses muros são quadrados. Questiono sobre o que geralmente fazemos antes de construir um muro (deixo no ar para fluir a conversa e ficar atento as falas, discussões e hipóteses que surgem). Geralmente, cavar, fazer vigas ou alicerces é o que surge nas falas deles. Indago para saber qual é a função do alicerce. Peço então para construírem um muro quadrado com dois quadradinhos de alicerce. Para isso, eles já tem em mãos a folha quadriculada, tesoura e lápis de cor. Informo que cada quadradinho da folha será nossa representação de tijolo. Saliento que para a construção do muro o alicerce deve ser incluído, assim conseguiremos ter um muro quadrado.
Então teremos:
2 x 2 = 2² = 4 (total de tijolos) – repete duas vezes o 2.
altura do muro base do muro
Bom, fica muito difícil explicar e usar setas aqui no Blog, mas a figura abaixo é uma cópia do meu planejamento. Vocês poderão ver melhor como a ideia é construída aos poucos. Os alunos pintam o alicerce salientando-o, destacam esse muro quadrado 2 por 2 recortando-o e o colam no caderno. Sendo que toda a explicação acima é feita também no quadro, onde eles copiam o esquema ao lado da figura colada.
2º MOMENTO:
Peço para construírem outro muro quadrado usando as folhas fornecidas (se faltar forneço outra). Agora um muro quadrado de 3 tijolos de alicerce. Peço para colorirem o alicerce e recortar o muro. Fazemos então, o esquema no quadro e posteriormente eles copiam ao lado da figura colada no caderno:
3 x 3 = 3² = 9 (total de tijolos) – repete duas vezes o 3.
altura base
alicerce = base = 3 tijolos
Reparem que nas figuras abaixo está bem explicado, inclusive quando falo no número que vai acima do 2 ou do 3 (base). Nestes exemplos reparem que coloco no esquema que faço no quadro o respectivo nome: expoente. Saliento qual é o seu significado:
dimensões do muro=comprimento e altura
Isso é feito até chegarmos no muro com alicerce de 10 tijolos.
Representação do muro de 2 cm x 2 cm até 5 cm x 5 cm.
Representação do muro de 6 cm x 6 cm até 8 cm x 8 cm.
Representação do muro de 9 cm x 9 cm até 10 cm x 10 cm.
Aqui está o material que uso na construção do muro concretamente. Como citei, os tijolos vermelhos representam o alicerce. Quando eles vão fazendo na folha quadriculada eu vou fazendo concretamente usando os cubos de madeira. Teve um ano que usei o Material Dourado para isso. Mas são muito pequenos, por isso acho melhor cubos grande e coloridos. Este material salienta melhor a base, a composição total do muro e a altura. O aluno tem a oportunidade de visualizar bem cada definição e conceito.
Representação do muro 5 cm x 5 cm – com alicerce/base em vermelho.
Abaixo uma aluna destacando a base, a composição total do muro e sua altura, concretizando os conceitos aprendidos. Os alunos também se dirigem à mesa para manusearem o material e refazerem as atividades usando os cubos, assim comparam com o que construíram e colaram no caderno.
Representação do muro 4 cm x 4 cm – com alicerce/base em vermelho.
4 altura x4 comprimento=4²= 16 tijolos
Depois de construída a ideia de potenciação. Ter feito esclarecimentos de qualquer dúvida que tenha surgido. Retomado todo o processo novamente, com questionamentos, perguntando de novo: O que é o alicerce(base)? O quesignifica o expoente 2? Quantas dimensões possuem o quadrado? A que isso está atrelado? Esclarecendo novamente que o expoente denomina-se QUADRADO devido a figura ter DUAS DIMENSÕES. Lemos:quatro ao quadrado = 4². Passamos então para fazer atividade de fixação. Utilizo folhas de ofício quadriculadas e também exercícios no quadro.
3° MOMENTO:
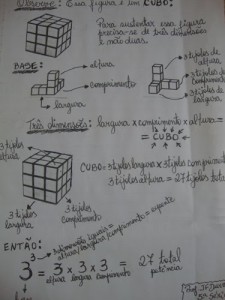
Neste momento faço a introdução do expoente 3. Para isso fiz um resumo em uma folha e forneço a cópia para eles. Mas antes, construímos a ideia usando os cubos. Lembro que para sustentar o cubo precisamos mais dimensões que o muro quadrado construído anteriormente. Começo mostrando um dos cubo. Falo dos lados (quantidades), das faces, das arestas. A maioria do alunos olhando as peças lembram do famoso DADO. Neste momento saliento as dimensões que um cubo apresenta. Aproveito também para lembrar que quando estávamos construindo os quadrados nós desconsiderávamos uma das dimensões do cubo. Mostro que ao juntarmos outros cubos podemos fazer cubos maiores. É aí que começo a usar as duas cores (vermelho e amarelo) para salientar as dimensões que os cubos maiores apresentam. Abaixo a folha que forneço aos alunos. Repare que saliento bem a composição da base nesse caso:
base = altura, comprimento e largura
Três dimensões = altura x comprimento x largura =CUBO
As fotos seguintes, mostram bem o processo de construção. Reparem que tento fazer passo a passo. Primeiro faço a altura, depois o comprimento e por último a largura (usando cubos vermelhos). Pergunto para eles o que devo fazer para que essas dimensões formem então um cubo maior. Usando os cubos amarelos vou preenchendo e perguntando: – E agora, é um cubo? Vou preenchendo até concordarem que formamos um grande cubo.
Veja as dimensões em vermelho.
Três dimensões = 2alturax 2comprimento x 2largura
Veja as dimensões em vermelho, sendo preenchido com cubos amarelos para formar o cubo maior.
Finalizado, temos:
2 de alturax 2 de comprimento x2 largura=2³=8 tijolos
Veja o cubo se formando com as dimensões bem salientadas.
O cubo maior quase preenchido com os cubos amarelos.
Aqui bem salientada as dimensões em vermelho e o cubo maior todo preenchido. Fica bem nítida a altura, comprimento e a largura.
Neste caso:
3 de alturax3 de largurax 3 de comprimento=3³=27 tijolos
São três dimensões, portanto está relacionado a figura de um cubo. Por isso o expoente nesse caso nomeia-se CUBO. Lemos: três ao cubo = 3³.
A leitura, a representação, a nomenclatura, os cálculos e algumas observações são feitas resumidamente no quadro, retomando a explicação para que eles copiem o esquema que ficará registrado no caderno.
Faço uma observação que não canso de repedir:
2³ = 2 x 3 NÃO PODE!!!!!
Os alunos fazem muito esse equívoco. É aí que lembro e também me uso do material dos cubos para mostrar e pergunto:
2³ (dois ao cubo)
quantos cubos obtemos no total?
Monto o cubo com as dimensões contendo – 2 de altura, 2 de comprimento e 2 de largura, e preencho o resto com cubos amarelos. Então,
São 6 no total????
NÃO!!!
SÃO 8 CUBOS!!
Lembro que o expoente avisa quantas vezes a base é multiplicada. Repito com vários exemplos aproveitando o material, pois eles se equivocam inúmeras vezes. Mostro que usando o material concreto ajuda muito em amenizar o erro, pois fica bem nítida a compreensão das dimensões envolvidas, quantas são e o que resulta dessa operação. Abaixo a explicação no meu diário do esquema que realizo no quadro negro.
Abaixo uma cópia de um trabalho. Aqui formatei a ideia em exercícios, em que os alunos deveriam: pintar a base do quadrado e do cubo; escrever na forma de potências as figuras; e colocar o resultado da potência.
MENTO:
RADICIAÇÃO
Na Radiciação mostro no concreto a operação inversa. DESCONTRUÍMOS OS MUROS e DESCONTRUÍMOS OS CUBOS montados. Isso mesmo! Como a Radiciação é a operação inversa da Potenciação, utilizo os muros quadrados construídos anteriormente e mostro que, o que procuramos com a radiciação é descobrir QUAL É A BASE que ORIGINOU esse muro, isto é, QUAL É O ALICERCE, ou ainda, QUANTOS TIJOLOS FORMAM O ALICERCE DESSE MURO. PORTANTO, SE TEMOS UM MURO FEITO POR 64 TIJOLOS, QUANTOS TIJOLOS COMPÕES O ALICERCE DESSE MURO?
sinal do radical: mostro historicamente a evolução e o motivo do símbolo;
índice: 2 ou 3 – explico que é referência ao muro quadrado ou a figura do cubo;
radicando: total de tijolos do muro ou do cubo grande;
raiz: número de tijolos do alicerce = base – bidimensional (muro) – tridimensional (cubo).
Nesse momento mostro historicamente o significado do sinal do radical. Como ele surgiu, como foi a evolução do sinal. Percebemos então, que a base desse muro é feita de 8 TIJOLOS. Então, a RAIZ QUADRADA DE 64 É 8. Um MURO QUADRADO composto de 64 TIJOLOS, tem de ALICERCE, 8 TIJOLOS. Assim, também concluímos quando temos a RAIZ CÚBICA. RAIZ CÚBICA DE 64 É 4. Por que? PORQUE SÃO NECESSÁRIOS 4 CUBOS PARA SUSTENTAR AS DIMENSÕES, ISTO É, A BASE TRIDIMENSIONAL QUE COMPÕE ESSE GRANDE CUBO. Mostro tudo isso através do material que tenho, tudo concretamente e sempre fazendo paralelamente referência ao material que possuem colado no caderno. Faço no quadro um esquema com nomenclaturas e outros exemplos aproveitando o momento para explicitar e esclarecer dúvidas que vão surgindo. E assim então pessoal, que transcorre toda minha aula sobre Potenciação e Radiciação.