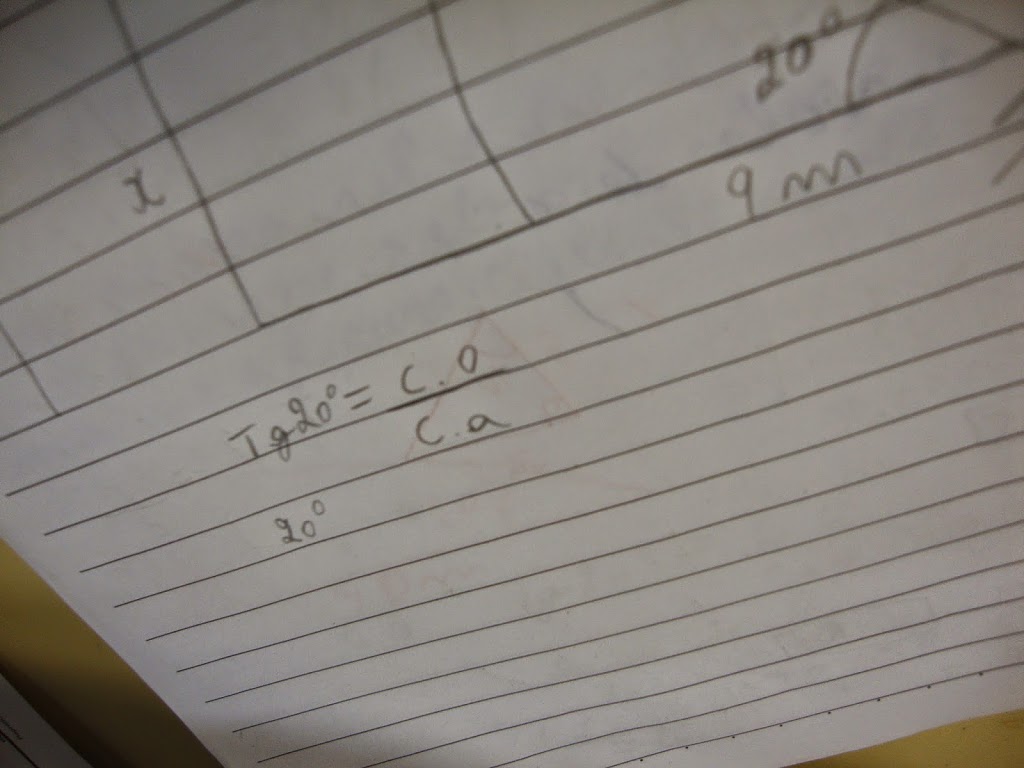02/06/2014
No 2º ano do Ensino Médio Surdo no Instituto Estadual de Educação Assis Brasil – Pelotas/RS, estou iniciando o conteúdo de TRIGONOMETRIA. Para dar início ao tema, salientei que a palavra TRIGONOMETRIA é formada por três radicais gregos:
TRI ► (três)
GONOS ► (ângulos)
METRON ► (medir)
Daí vem seu significado mais amplo: Media dos Triângulos, assim através do estudo da TRIGONOMETRIA podemos calcular as medidas dos elementos do triângulo (lados e ângulos). E que com o uso de triângulos semelhantes podemos calcular distâncias inacessíveis, como a altura de uma torre, a altura de um edifício, a distância entre duas ilhas, o raio da terra, a largura de um rio, entre outras possibilidades.
Depois de ter dados os conceitos básicos e alguns exercícios, mostrei algumas aplicabilidades da teoria na prática. Perguntei para eles se já tinham visto alguém com um aparelho como se fosse um telescópio geralmente montado nas estradas ou em campos. Esclareci que esse aparelho tem o nome de TEODOLITO. Que é um instrumento de precisão óptico que mensura ângulos verticais e horizontais, aplicado em diversos setores como na construção civil, na navegação, na agricultura, etc. Levei o computador e mostrei o vídeo abaixo que me pareceu bem esclarecedor sobre a função do instrumento e também porque o vídeo vem com legenda.
Depois de ter visto o vídeo mostrei um TEODOLITO CASEIRO feito por mim, usando um transferidor, carcaça de uma caneta, cordão, uma porca e fita adesiva. Foto abaixo:
Um dos alunos assegurou o parelho nas mãos e eu usando outro TEODOLITO mostrei de que ele era composto e como funcionava. Deixei claro que o cordão deveria estar posicionado onde estava marcando 90º. Mas que para o aparelho funcionar teríamos que zerar esse valor e considerar 0º. Expliquei o motivo: dessa forma poderíamos marcar o ângulo no momento da inclinação do aparelho quando fosse fazer a “mira”. Mostrei a função da carcaça da caneta e como deveria proceder para a marcação do ângulo no momento da “mira”.
Para praticarmos fomos para o pátio da escola. Escolhemos um lugar bem iluminado e um prédio acessível para medir. Os alunos resolveram medir a altura do prédio que está na primeira foto abaixo, já que oferecia um bom espaço e uma boa liberdade para realizar as medições necessárias. Os alunos levaram o caderno e lápis para realizar as anotações.
Primeiro focamos o ponto onde eles ficariam para realizar a “mira”. Bem em frente ao ponto mais alto do prédio. Marquei com giz o ponto no chão. Logo após, o aluno mediu da base da parede até esse ponto na qual realizaria “mira”.
Encontram 9 m de distância entre a base da parede até o ponto de “mira”.
Abaixo, aluno fazendo a medição do ângulo usando o TEODOLITO CASEIRO. Fizemos três tentativas de medida para que eles se apropriassem e manuseassem o instrumento.
Depois de ter feitos as medições no pátio voltamos para a sala de aula e um dos alunos mediu a altura do outro aluno que utilizou o TEODOLITO na medição do ângulo.
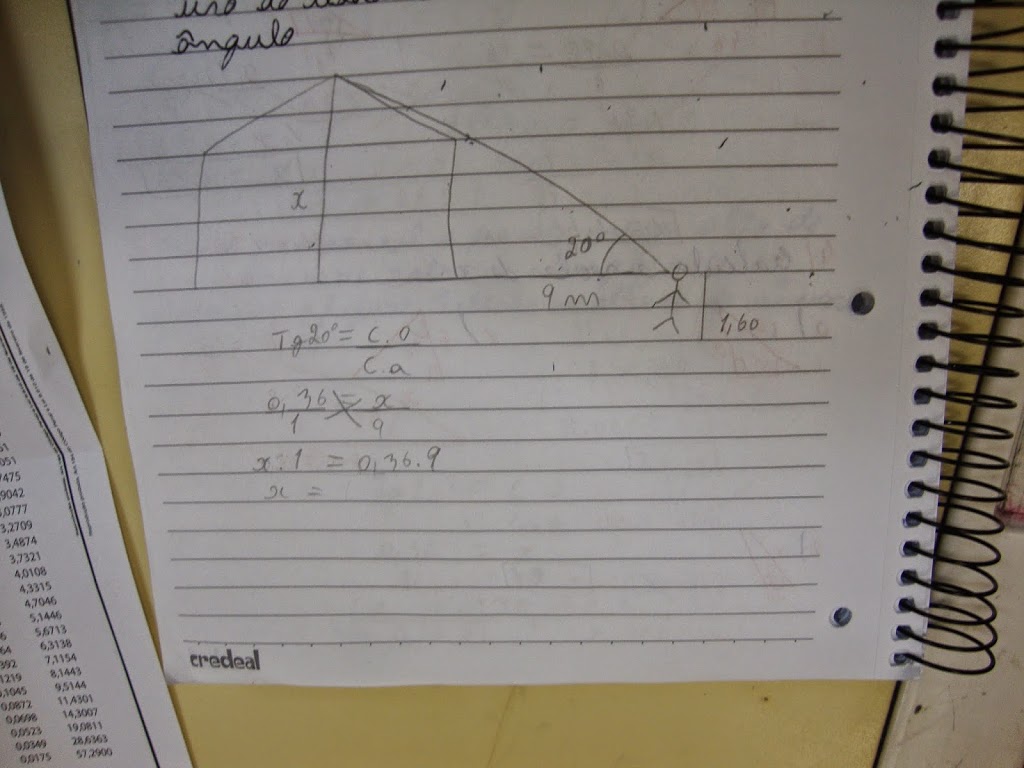
Feito isso, passamos todas as informações coletadas para o caderno. Pedi que desenhassem a parede, o ponto de posição da “mira” com todos os valores encontrados.
Valor de ângulo encontrado: 20º
Distância da base da parede até o ponto de “mira”: 9 m
Altura do observador: 1,60 m
Os alunos procuraram a relação trigonométrica que poderia ser usada para o cálculo da altura da parede e posteriormente o valor da tangente de 20º na tabela fornecida realizando todos os cálculos necessários. Fiquei muito feliz em perceber que não precisaram da minha ajuda para desenvolver esses cálculos. A única coisa que alertei, foi para não esquecerem de somar ao valor encontrado a altura do observador.
Expliquei que o material utilizado era caseiro, portanto, as medidas não era exatas. Mas que poderíamos fazer uma estimativa do valor encontrado: ± 5 m.
Outras possibilidades de construção de um TEODOLITO CASEIRO:
16/06/2014
Hoje expliquei o que era círculo, circunferência, arco e suas medidas. Mostrei usando um transferidor as medidas em GRAUS, GRADOS e RADIANOS e suas diferenças Fiz uma tabela mostrando os valores de cada um e expliquei que iríamos usar mais o radiano nesse conteúdo. Utilizei o transferidor para os alunos entenderem os ângulos mais usados: 90º, 180º, 270º, 360º/0º e seus valores correspondentes em radianos para concretizar mais as divisões feitas e seus valores.
23/06/2014
Semana de Aniversário da Escola.