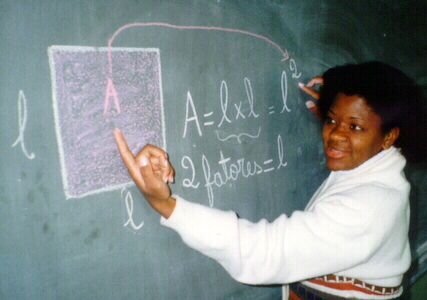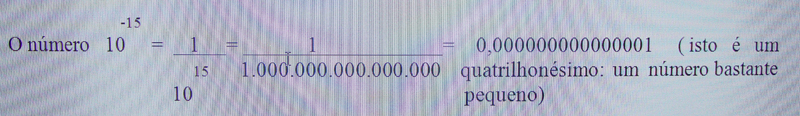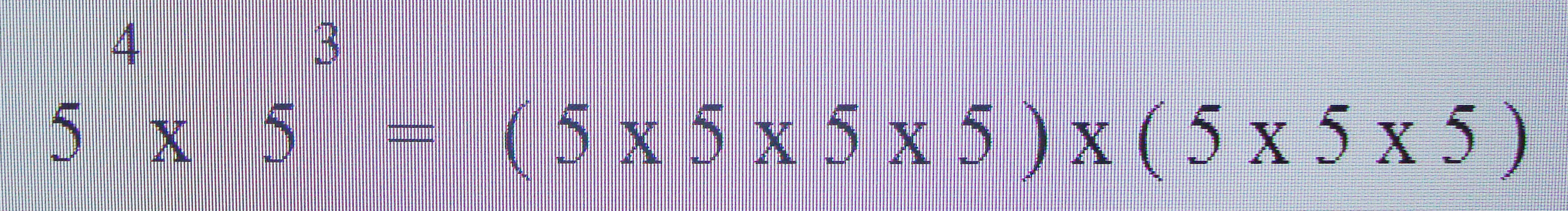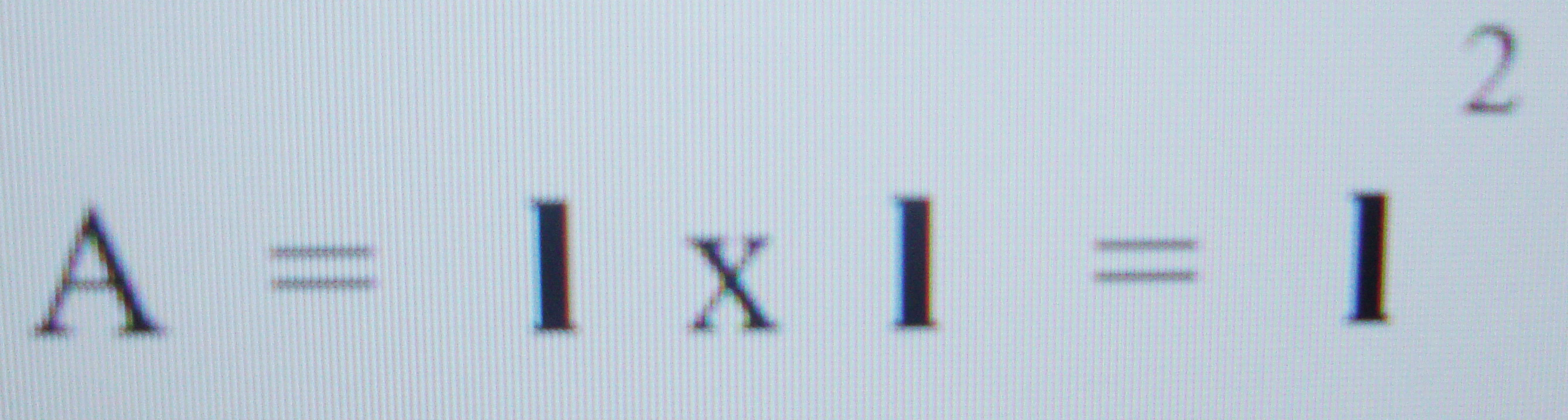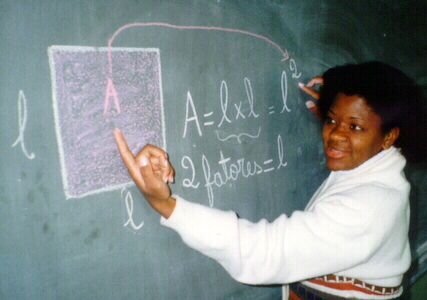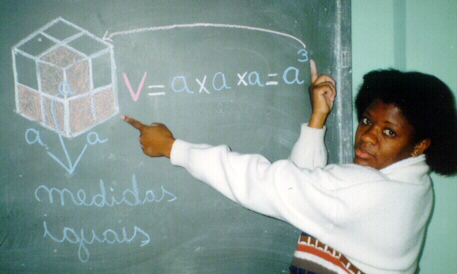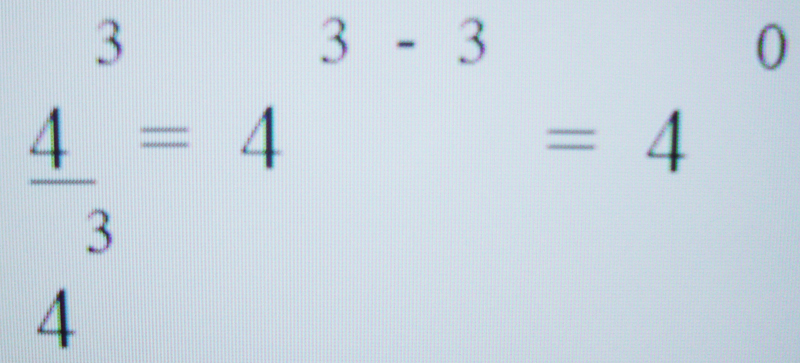POTENCIAÇÃO: UMA ANÁLISE ALGÉBRICA E GEOMÉTRICA
PARA O ENSINO FUNDAMENTAL
José Francisco Duran Vieira*
Artigo de minha autoria apresentado no Curso de Especialização na FURG/1999
RESUMO
Tentando resgatar a dicotomia criada entre a álgebra e a geometria, pretendo, com este artigo, desenvolver de forma clara e objetiva o assunto de potenciação. Direcionado ao ensino fundamental, este artigo vai mostrar a relação existente entre a álgebra e sua representação geométrica. Para isso, serão desenvolvida formas geometricamente concretas que determinarão essa relação. Pretendo transparecer numa visão ampla e simples para o professor do ensino fundamental essa dicotomia, auxiliando-o na tarefa da concreticidade do seu trabalho.
PALAVRAS-CHAVE: álgebra, geometria e novos métodos
ABSTRACT
Trying to rip apart the dicothomy created between algebra and geometry, I intend, with this article develop in a clear and objective way the matter of potentiality. Directed towards high schoolers, this article will show the relationship between Algebra and its geometric representation. So it can be done, geometrically concrete forms will be developed that will determeine said relationship. I intend to schow an ample and simple view of the matter for the high school teacher said dicothomy, helping him in the work of the concretionary of his work.
KEY WORDS: algebra, geometry its a new metodology
INTRODUÇÃO
# O que é potência de um número?
# O que é dois elevado na quarta potência?
# Qual é a origem do conceito de potência em Matemática?
# Por que dizemos que o número multiplicado por ele mesmo é um número elevado ao quadrado?
Essas questões devem fazer refletir sobre a prática pedagógica diante de uma conjuntura criada, onde evidencia-se a abstração ante um planejamento sem direcionamento construtivo. Perguntas que ficam muitas vezes no “ar” e que geralmente não são resgatadas numa forma simples e concreta, relacionando a forma algébrica, que na sua maior parte fica no abstracionismo, sem concreticidade, compartimentalizada e sem continuidade, com a geometria, proporcionando no aluno um desinteresse, e cujo enlace, muitas vezes existente, possibilitaria um leque de abrangência maior e uma visão ampla para um entendimento e difusão das ideias em sua totalidade. Por isto, este artigo sustenta-se na objetividade desse resgate, proporcionando ao professor do ensino fundamental, subsídios que nutram numa forma definida, a utilização da potenciação e a relação geométrica que nela existe.
A IDEIA DE “POTENCIALIZAR”
Muitas vezes as coisas criadas pelo homem vão se transformando com o uso até perderem ou ampliarem seu sentido original. Assim como uma ferramenta, que com o passar do tempo, vai se modificando e aprimorando sua utilidade, proporcionando uma facilidade no seu manuseio, as transformações tendem a potencializar ou tornar mais capacitado um determinado objeto ou situação. “A potência dá ideia de coisas grandes. Potencializar é aumentar.”1
Vamos utilizar a agricultura como exemplo: imagine duas áreas iguais onde se cultivem arroz, a base, ou seja, a área cultivada será a mesma, mas a produtividade de cada uma delas pode ser diferente, bastando para isso, que uma das áreas seja potencializada pelo uso de máquinas, fertilizantes e adubos. Neste caso, a tecnologia agrícola exerceria como um expoente dessa base. Os carteiros que entregam a correspondência em nossas casas, fazem esse trabalho a pé, mas já há algum tempo, os correios também passaram a usar motocicletas. Esta é uma forma de potencializar, de aumentar a capacidade de entrega da correspondência. Utilizando-se também de meios de transporte com maior capacidade, como caminhões aviões e outros, habilitaram num desempenho maior, a capacidade de entrega dos correios, e com isto, puderam atingir também, um aumento na área de atendimento. Na matemática, a palavra potência também está na sua origem ligada a ideia de números muito grandes, de grandes quantidades. Veja o exemplo:
A noção de potência foi se transformando com o passar do tempo, foi aos poucos sofrendo alterações. E isso que acontece com as ferramentas criadas pelos homens. O significado original vai sendo modificado com o próprio uso da ferramenta, de tal modo que com as potências nós também podemos representar quantidades muito pequenas. Veja o exemplo:
A grande vantagem do uso de potências está na facilidade de se realizar operações com elas. Números grande ou números pequenos com os quais seriam difíceis de trabalhar, ficam mais simplificados quando escritos na forma de potências. Veja:
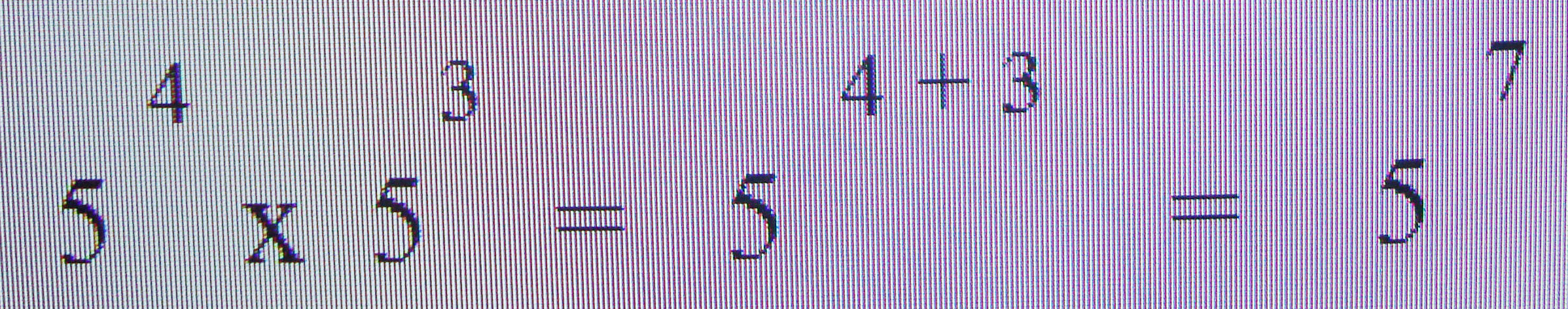
Para multiplicar essas duas potências de base 5, basta apenas somar os seus expoentes. Esta é uma das propriedades da potência que podemos utilizar, para facilitar os cálculos.
Generalizando, temos:
A sentença matemática representada algebricamente é uma identidade, pois ela vale sempre.ORIGEM DA POTENCIAÇÃO NA MATEMÁTICA
Existem várias situações em que nós devemos multiplicar um número por si mesmo sucessivas vezes.
Existem várias situações em que nós devemos multiplicar um número por si mesmo sucessivas vezes.
Observe a foto(1):
 Foto (1) |
Para calcular a área de um quadrado cujo lado tem medida l, devemos multiplicar l x l.
Assim, podemos representar algebricamente a situação:
 (isto significará a unidade de área) |
Resgatamos com isto, uma das perguntas inicialmente feita neste artigo:
# Por que dizemos que o número multiplicado por ele mesmo é um número elevado ao quadrado?
 Foto (2)
|
Note com isto, que a expressão elevado ao quadrado está associada a área do quadrado. Foto(2).
QUANDO O EXPOENTE FOR 3
Fazendo uma reflexão diante do que foi anteriormente exposto, qual a relação que podemos fazer quando um número é elevado na terceira potência?
Fazendo uma reflexão diante do que foi anteriormente exposto, qual a relação que podemos fazer quando um número é elevado na terceira potência?
Observe a foto(3):
 Foto (3) |
Repare que a figura possui três dimensões (tridimensional): comprimento, largura e altura. Suas medidas são iguais. Consequentemente a figura geométrica formada é um cubo. Esse cubo, composto por outros cubos que estão contidos dentro dele, formando um grande cubo, conforme mostra a foto(4).
 Foto (4) |
Observe que para montarmos este cubo, precisamos na sua base, agora tridimensional (comprimento, largura e altura), dois cubos menores (suas medidas correspondem a 1 unidade de comprimento), que irão compor a base desse cubo grande, totalizando duas unidades de comprimento em sua base. Se representarmos essa medida (as duas unidades de comprimento) por a –foto(5) – para obtermos o volume desse cubo devemos multiplicar a x a x a, um produto com três fatores iguai a a.
 Foto (5) |
Assim:
 Foto (6) |
Percebe-se, então, nessa relação, que a expressão elevado ao cubo está associada o volume do cubo. Foto(6).
ALGUMAS CONSIDERAÇÕES
O que é potência de um número?
“As potências são formas abreviadas para indicar multiplicações com fatores todos iguais….” 2
A potenciação surgiu dessa necessidade, assim, por exemplo:
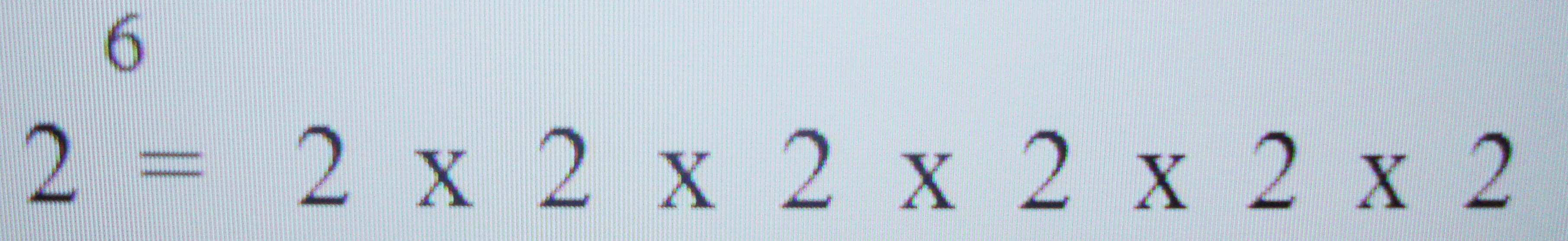
O que é potência de um número?
“As potências são formas abreviadas para indicar multiplicações com fatores todos iguais….” 2
A potenciação surgiu dessa necessidade, assim, por exemplo:
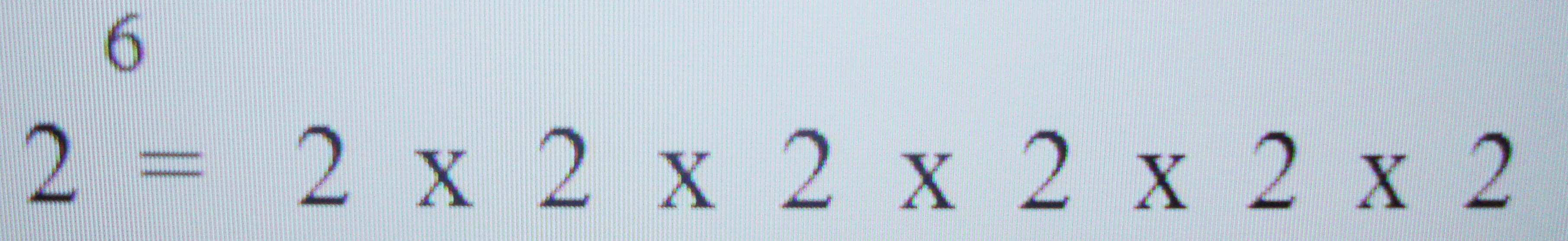
Generalizando essa ideia, temos:
Se a potenciação surgiu da necessidade de representar produtos de fatores iguais, e esses fatores devem ser naturais maiores ou iguais a dois, como podemos ter produto com apenas um fator? E produto com zero fator? Imagine então um produto com cinco fatores e meio? E um produto com menos sete fatores? Como isso tudo surgiu? De que necessidade? O conceito de potenciação surgiu de uma forma e que posteriormente fazendo reflexões e questionamentos, esses conceitos aos poucos foram sendo alterados, dando origem as regras que regem hoje a potenciação. Regras que servem muitas vezes para darmos um significado, de tal forma que as definições que anteriormente não valiam passem a valer. Como por exemplo, um produto com um só fator. Assim, leis gerais com uma abrangência maior foram construídas. Veja uma delas:
Generalizando esta ideia:
Para dividir duas potências de mesma base, devemos conservar a base e subtrair os expoente. Seguindo esta ideia, analise o exemplo dado:
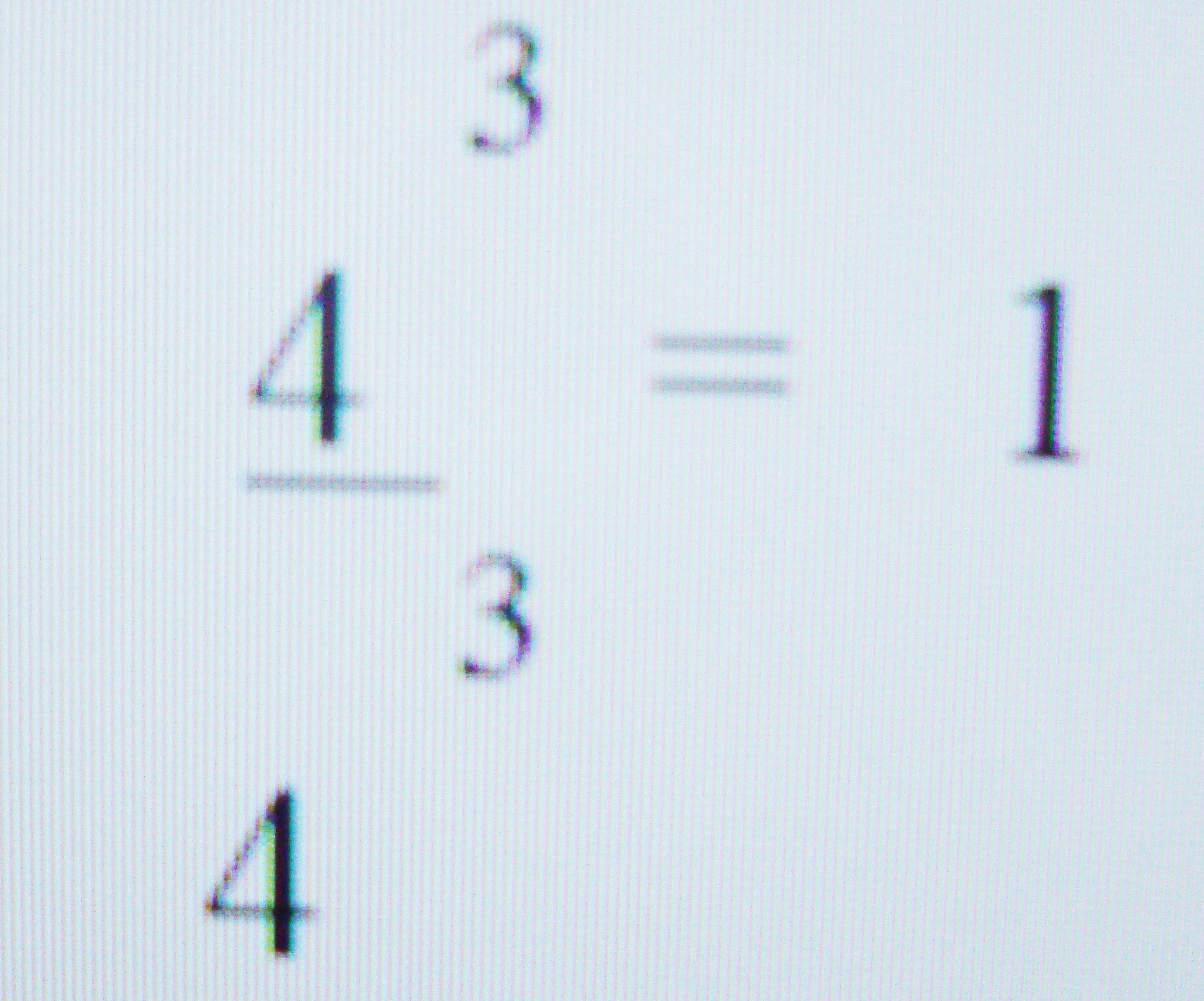Repare que estamos dividindo um número por ele mesmo e esse resultado (quociente), é sempre igual a 1. Como podemos representar essa mesma divisão usando a regra da divisão de potências? Observe:
Mas como? Um produto com zero fator? Por isso que os conceitos iniciais utilizados com o passar do tempo ficaram restritos e então, formas gerais e convenções foram criadas e com isto foram alterando-se as regras, dando uma abrangência maior aos conceitos e as definições e assim, serem toleradas e aceitas como verdadeiras. Essa é a única forma de se entender o que é uma potência de expoente zero. É impossível compreender o que é 4º pensando-se num produto de fatores iguais, pois como pode existir um produto com zero fatores? Essa definição que é abstrata, só será compreendida de tal modo que uma regra que não se aplicava a um caso possa ser usada também nesse caso, dessa forma tornando a regra mais geral. Foi assim que se definiu então que:
“Todo número natural não-nulo elevado a 0 é igual a 1”. 3
Como você definiria uma potência cujo expoente é um? Ou uma potência fracionária? E potências que possuem expoentes maiores do que dois, que figuras elas formariam? Existem nomes especiais também para esses casos? Você já pensou nisso? Como poderíamos resgatar a radiciação (operação inversa da potenciação), partindo destas idéias? Por que ela é a operação inversa? Reflexões como estas elevam a dinâmica do trabalho e despertam nos alunos a curiosidade, enfatizando a construção do conhecimento e proporcionando ao aluno reflexões que o levarão a entender as relações existentes entre a álgebra e a geometria.
CONCLUSÃO
Partindo da ideia que devemos provocar reflexões que despertem em nosso professor o interesse de proporcionar ao aluno toda a forma de “aprender pensando”, e motivar no próprio professor condições que o levem a metamorfosear suas ideias, conclui-se que o resgate aqui feito traz à tona, num amplexo único, essa essência. Sustentada na concreticidade e na clareza, esse resgate resguarda oportunidades de desenvolver trabalhos mais abrangentes e que podem ser ampliados para outros conteúdos, como: área, volume, radiciação (já citada anteriormente) e outros. Fornecendo ao aluno uma visão clara e principalmente de uma continuidade, uma uniformidade historicamente existente mas que com o passar do tempo foi desprendendo-se, e o abstracionismo ocupando um lugar de destaque numa forma de ensino por “gavetas”, onde desconsidera-se essa unificação, travando qualquer forma de pensamento reflexivo e construtivo.
* Professor do Curso Normal Formação Educação Infantil do Colégio Municipal Pelotense – Pelotas/RS – Brasil.
_______
1. Jornal do Telecurso 1º Grau, pág. 45, 1989.
2. Jornal do Telecurso 1º Grau, pág. 47, 1989
3. Matemática, Giovanni & Giovanni Jr., FTD, 1996.